previous <<==>> next
ARISTO - HYPERBOLOG ( 25 cm Scales )
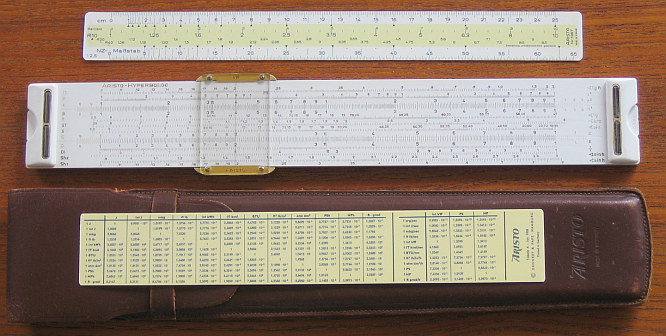
ARISTO-Werke Dennert & Pape, Hamburg / Germany (1958)
*******************************************************************
S C A L E S of the ARISTO » HYPERBOLOG « Model 0971
===================================================================
Front Side [ inverse / RED ] Back Side
===================================================================
[LL01] [exp(-0.01X)]
[LL02] [exp(-0.1X)] Th <0.1 .. 3> TanH(0.1X)
[LL03] [exp(-X)] K X3
DF πX A X2
-------------------------------------------------------------------
CF πX B X2
[CIF] [1/πX] T tan(0.1X);[cot(0.1X)]
L lgX ST arc(0.01X)
[CI] [1/X] S sin(0.1X);[cos(0.1X)]
C X C X
-------------------------------------------------------------------
D X D X
LL3 exp(X) [DI] [1/X]
LL2 exp(0.1X) Sh2 <0.85 .. 3> SinH(X)
LL1 exp(0.01X) Sh1 <0.1 .. 0.9> SinH(0.1X)
R E M A R K S :
===================================================================
Production Code = 58_2 = Hamburg, 1958, Lot 2
The DEFINITIVE FORMS for the HYPERBOLIC FUNCTIONS are:
CosH(X) = ( exp(+X) + exp(-X) ) / 2 <== this is the "Chain Line"
SinH(X) = ( exp(+X) - exp(-X) ) / 2 ( eg. suspension bridge )
TanH(X) = SinH(X) / CosH(X)
exp(X) = SinH(X) + CosH(X)
1 = CosH2(X) - SinH2(X)
CosH(X) = SinH(X) / TanH(X) = sqrt( 1 + SinH2(X) ) = H(X)
Using the Hyperbolic Functions:
Start with value on the Sh scales ==>> reading SinH on D scale,
start with value on the D scale ==>> reading ArcSinH on Sh.
Start with value on the Th scale ==>> reading TanH on D scale,
start with value on the D scale ==>> reading ArcTanH on Th.
The SR came in a leather case together with the »1367« RULER with
"Norm Zahlen" = NZ = "Standard Number Sequences" and »Tabelle-A«
with CONVERSION-TABLES.
Historical Remarks ...
impressum:
*******************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 08/30/14
|