Die Eigenschaften der Zykloide aus mathematischer, physikalischer und historischer Sicht
Zusammenfassung der Diplomarbeit von Diana Heuer WS 2003 E-Mail: ![]()
Betreuerin:
Prof. Dr. Angela Schwenk-Schellschmidt
Gutachter:
Prof. Dr.-Ing. Martin Ochmann
Aufgrund ihrer vielen besonderen und schönen Eigenschaften steht in dieser Arbeit eine einzige Kurve, die Zykloide, im Mittelpunkt. Anhand dieser Kurve, die auch unter dem Namen "Helena der Geometer" bekannt ist, wurden ihre zahlreichen Eigenschaften (unterteilt in zwei große Kapitel; die mathematischen und physikalischen Eigenschaften) untersucht.
Beim Studium der heutigen Literatur fällt auf, dass die Zykloide mehr und mehr in Vergessenheit gerät. Kaum ein Mathematiker ist sich der Schönheit und der Eleganz der älteren Arbeiten in Bezug auf die Zykloide bewusst. Während wir heute das schnelle Ergebnis mit minimalen Zeitaufwand und mit Hilfe der neuesten Methoden suchen, sind die historischen Arbeiten durchzogen von alteingesessener Geometrie und genialen Ideen. Während die Zykloide damals den meisten Gelehrten vertraut war, so ist sie heute gerade noch den Geometern und den Physikern bekannt. Darüber hinaus verschwindet sie mehr und mehr aus der gängigen Literatur. War die Zykloide in älteren Büchern immer Bestandteil zahlreicher Beispiele und Aufgaben, so wird sie heute gerade kurz erwähnt und Untersuchungen übersteigen kaum die Grenze des Flächeninhaltes und der Bogenlänge. Dies ist in Anbetracht der Tatsache, dass die Zykloide so zahlreiche schöne Eigenschaften besitzt, sehr bedauerlich.
Diese Arbeit verbindet mathematische und physikalische Betrachtungen mit den historischen Werken. Sinn und Zweck war es, die Betrachtungsweisen der Mathematiker in den früheren Jahrhunderten darzulegen und die Ergebnisse mit den heutigen Methoden nachzuvollziehen. Viele Betrachtungen von damals zogen die Entwicklung neuer mathematischer Teilgebiete nach sich, wie zum Beispiel die Entwicklung der Variationsrechnung, die im berühmten Brachistochronenproblem ihren Anfang fand.
In dieser Arbeit stoßen wir auf viele uns bekannte Mathematiker und Physiker. Erwähnenswert sind die Darstellungen und Lösungen von Jacob- und Johann Bernoulli, Blaise Pascal, Christian Huygens, Isaac Newton, Gottfried Wilhelm Leibniz sowie Galileo Galilei.
Mit den folgenden ausgewählten kleinen Darlegungen soll ein kleiner Einblick in diese Arbeit gewährt werden. Sie werden ohne jegliche Beweise zitiert.
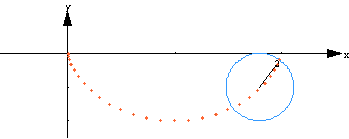
Abb. 1: Parametrisierung der Zykloide |
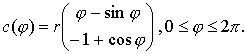
1. Beziehung zwischen Roll- und Tangentenwinkel
Bezeichnet ![]() mit
mit ![]() den Winkel, den die Tangente an die Zykloide mit der x-Achse einschließt, und
den Winkel, den die Tangente an die Zykloide mit der x-Achse einschließt, und ![]() wie üblich den Rollwinkel des Kreises, der die Zykloide erzeugt, so gilt zwischen beiden Winkeln der folgende Zusammenhang:
wie üblich den Rollwinkel des Kreises, der die Zykloide erzeugt, so gilt zwischen beiden Winkeln der folgende Zusammenhang: ![]() .
.
2. Tangente der Zykloide
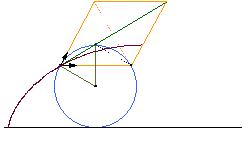
Abb. 2: Tangente der Zykloide |
Das Anlegen einer Tangente an eine Kurve war bis zu der Entwicklung der Differentialrechnung durch Leibniz und Newton ein beliebtes Problem unter den Mathematikern in den früheren Jahrhunderten. Bei der Zykloide geht die Tangente durch den Scheitelpunkt des Rollkreises in der zugehörigen Lage.
3. Bogenlänge der Zykloide
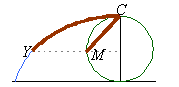
Abb. 3: Bogenlänge der Zykloide |
Blaise Pascal vergleicht Teile des Bogens mit den entsprechenden Sehnen am beschreibenden Kreis. Es stellt sich heraus, dass der Bogen genau doppelt so lang ist wie die zugehörige Sehne:
Bei einem Durchmesser von
4. Flächeninhalt der Zykloide
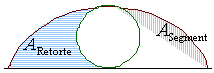
Abb. 4: Flächeninhalt der Zykloide |
Die Zykloidenretorte wird von Gottfried Wilhelm Leibniz eingeführt.
Er betrachtet spezielle Flächenstücke und wir erfahren, dass eine beliebige Zykloidenretorte genau die doppelte Fläche einschließt wie das entsprechende Segment: ARetorte=2ASegment .
Eine weitere bemerkenswerte Eigenschaft erfahren wir, wenn wir den Flächeninhalt einer ganzen Zykloidenretorte berechnen. Dort gilt nämlich ARetorte=
5. Flächensegmente an der Zykloide von Isaac Newton
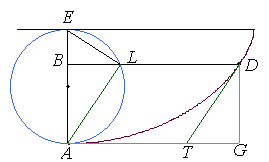
Abb. 5: Flächensegmente an der Zykloide von Isaac Newton |
Von Isaac Newton erfahren wir im Zusammenhang mit verschiedenen Flächensegmenten folgendes: AABLA=AAGDA . Sein Beweis ist eine elegante Anwendung für die von ihm entwickelte Infinitesimalrechnung
Er bestimmt
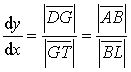 .
.
Das heißt, es gilt
6. Einhüllende der verkürzten Zykloiden
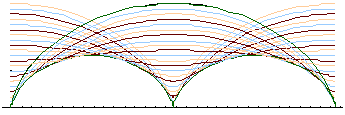
Abb. 6: Einhüllende der verkürzten Zykloiden |
Die Einhüllende ist eine Kurve, die mit jeder Kurve der Schar genau einen Punkt gemeinsam hat, in diesem Punkt ist die Tangentensteigung der Scharkurve identisch mit der Tangentensteigung der Einhüllenden.
Beim Betrachten der Kurvenschar aller verkürzten Zykloiden erhalten wir als Einhüllende wieder eine Zykloide, für diese gilt:
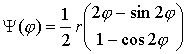 .
.
7. Evolute der Zykloide
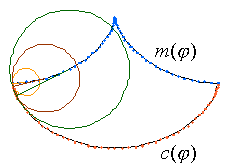
Abb. 7: Evolute der Zykloide |
Als weitere Besonderheit zeigt sich, dass die Evolute und die Evolvente einer Zykloide wieder Zykloiden sind. Als Evolute bezeichnen wir den Ort der Krümmungsmittelpunkte ebener Kurven. Die Tangenten der Evolute sind gleichzeitig Normalen der gegebenen Kurve.
Die Evolute der Zykloide hat die Darstellung
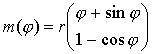 und das ist die Darstellung einer um
und das ist die Darstellung einer um 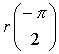 verschobenen Zykloide, die im tiefsten Punkt beginnt.
verschobenen Zykloide, die im tiefsten Punkt beginnt.
8. Evolvente der Zykloide
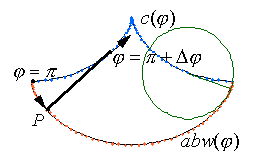
Abb. 8: Evolvente der Zykloide |
Die Evolvente ist diejenige Kurve, die ein Punkt P eines straff gespannten, eng an einer Kurve anliegenden Fadens beschreibt, wenn dieser abgewickelt wird. Die Kurve, die beschrieben wird, ist abhängig vom Ausgangspunkt, den wir auf der Kurve c(
Wir wählen unseren Punkt P an der nach oben geöffneten Zykloide c(
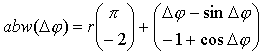 .
.
Die Evolvente einer Zykloide ist also eine um
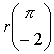 verschobene Zykloide.
verschobene Zykloide.
9. Tautochrone
"Bestimme die Bahnkurve, auf der ein hinabgleitender Körper den tiefsten Punkt unabhängig vom Startpunkt immer in derselben Zeit erreicht." Diese Aufgabe von Galileo Galilei bearbeitete der Niederländer Christian Huygens und er bemerkte als erster, dass Kugeln, die auf einer Zykloidenbahn hinabrollen, den tiefsten Punkt immer zur gleichen Zeit erreichen, egal aus welcher Höhe sie gestartet waren. Dies ist die Eigenschaft der Tautochrone. Mit der erhaltenen Zeit von 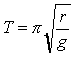 erkennen wir, dass die Fallzeit T eine von der Höhe H unabhängige Konstante ist.
erkennen wir, dass die Fallzeit T eine von der Höhe H unabhängige Konstante ist.
10. Zykloide durch spezielle Bogenlängenfunktion bestimmt
Suchen wir die Parameterdarstellung einer Kurve, die folgenden Eigenschaften hat:
- sie soll differenzierbar sein und sie soll im Koordinatenursprung beginnen. Ihre Steigung im Ursprung soll 0 betragen. Mit
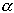 werde der Winkel bezeichnet, den die Kurventangente mit der x-Achse einschließt,
werde der Winkel bezeichnet, den die Kurventangente mit der x-Achse einschließt, - als Parameter in unserer Darstellung nehmen wir den Steigungswinkel
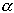 ,
, - bezeichnet s wie üblich die Bogenlänge, dann soll s(
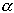 )=lsin(
)=lsin(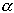 ) mit einer geeigneten positiven Konstante l gelten,
) mit einer geeigneten positiven Konstante l gelten,
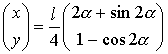 , und dies ist die Parameterdarstellung eines nach oben geöffneten halben rechten Zykloidenbogens. Damit stellen wir einen wichtigen Zusammenhang zwischen der Bogenlänge der Zykloide und dem Steigungswinkel dar, den Christian Huygens in der Darstellung seines Zykloidenpendels benutzt.
, und dies ist die Parameterdarstellung eines nach oben geöffneten halben rechten Zykloidenbogens. Damit stellen wir einen wichtigen Zusammenhang zwischen der Bogenlänge der Zykloide und dem Steigungswinkel dar, den Christian Huygens in der Darstellung seines Zykloidenpendels benutzt.
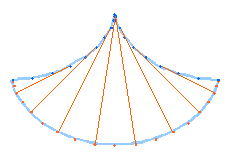
Abb. 9: Zykloidenpendel |
Huygens hat gezeigt, wie die tautochronen Bewegungen auf der Zykloidenbahn durch ein besonderes Fadenpendel, dem sogenannten Zykloidenpendel, realisiert werden können. Er behandelt die Frage, bei welcher Kurvengestalt die Schwingungsdauer unabhängig vom Winkel
11. Katakaustik einer Zykloide
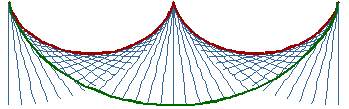
Abb. 10: Katakaustik einer Zykloide |
Fallen Lichtstrahlen in einen geeignet gekrümmten Spiegel, so bilden die reflektierten Strahlen eine zusammenhängende einhüllende Fläche, die Katakaustik.
Für die Zykloide ergibt sich
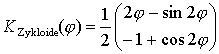 , das ist die Parameterdarstellung einer Zykloide mit dem Radius
, das ist die Parameterdarstellung einer Zykloide mit dem Radius 12. Brachistochrone
Das Problem der Brachistochrone ist das wohl bekannteste im Zusammenhang mit der Zykloide. Gefragt ist nach einer Kurve, auf der sich ein Körper unter dem Einfluss der Schwerkraft am schnellsten bewegt. Galileo Galilei hielt den Kreisbogen für die schnellste Verbindung.
Mit dem Vergleich der historischen Lösungen dieses Problems der Baseler Brüder Johann und Jacob Bernoulli belegen wir einen der vielen wissenschaftlichen Wettstreite unter den Mathematikern.
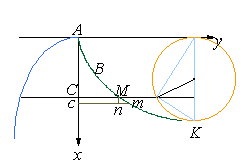
Abb. 11: Lösung des Brachistochronenproblems von Johann Bernoulli |
Die Differentialgleichung der Zykloide
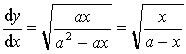 wurde schon in den ersten Schriften der Integralrechnung von Leibniz von 1686 gefunden und ist das Schlüsselergebnis in der Lösung von Johann Bernoulli. Hier sind allerdings die Rollen der Achsen vertauscht, wie in den früheren Arbeiten üblich.
wurde schon in den ersten Schriften der Integralrechnung von Leibniz von 1686 gefunden und ist das Schlüsselergebnis in der Lösung von Johann Bernoulli. Hier sind allerdings die Rollen der Achsen vertauscht, wie in den früheren Arbeiten üblich.
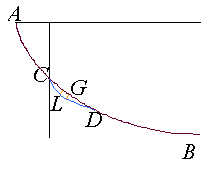
Abb. 12: Lösung des Brachistochronenproblems von Jacob Bernoulli |
Jacob Bernoulli zeigt in seinem Beweis, dass der gesuchte Bogen die Differentialgleichung
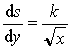 mit einer geeigneten Konstanten k erfüllt. Dann zeigt er, dass Zykloiden diese Differentialgleichung erfüllen, womit bewiesen ist, dass die Brachistochrone eine Zykloide sein muss.
mit einer geeigneten Konstanten k erfüllt. Dann zeigt er, dass Zykloiden diese Differentialgleichung erfüllen, womit bewiesen ist, dass die Brachistochrone eine Zykloide sein muss.
Das Hauptergebnis Jacob Bernoullis ist die Beziehung tCG+tGD=tCL+tLD, wobei tCG die Zeit ist, die für die Bewegung auf dem Bogen von C nach D benötigt wird. Diese Beziehung ist für Jacobs Argumentation ganz wesentlich. Sie gilt nur unter der Voraussetzung, dass der Bogen
Johann Bernoulli wie auch Jacob Bernoulli erhalten, wenn auch in anderer Schreibweise, die charakterisierende Differentialgleichung der Zykloide
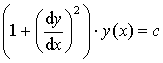 , (hier haben die Achsen wieder die gewohnte Richtung). Umgekehrt führt diese Differentialgleichung auf eine Zykloide mit dem Durchmesser
, (hier haben die Achsen wieder die gewohnte Richtung). Umgekehrt führt diese Differentialgleichung auf eine Zykloide mit dem Durchmesser 13. Vergleich verschiedener Laufzeiten
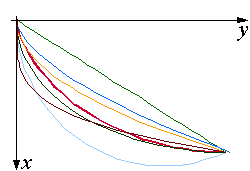 
Abb. 13: Vergleich verschiedener Laufzeiten |
Der Vergleich verschiedener Laufzeiten
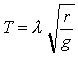 zeigt die Zykloide als die schnellste Bahn.
zeigt die Zykloide als die schnellste Bahn.
Unter den hier betrachteten Kurven ist die Gerade, die die kürzeste Verbindung zwischen beiden Punkten darstellt, die Kurve mit der längsten Laufzeit
14. Schattenwurf der Schraubenlinie

Abb. 14: Schattenwurf der Schraubenlinie |
Bei der Projektion der Schraubenlinie mit parallelem Licht ergibt der Schattenwurf eine Zykloide, wenn die Lichtstrahlen parallel zu einer Tangente der Schraubenlinie verlaufen. [weiteres zur Projektion]
Literatur
Allgemeine Literatur
[Bau] Baule, Bernhard; Die Mathematik des Naturforschers und Ingenieurs Band VII – Differentialgeometrie, S.Hirzel Verlag Leipzig, 1961
[Bro] Bronstein: Taschenbuch der Mathematik, Verlag Harri Deutsch, Frankfurt/Main 1979
[Doc] Do Carmo, Manfredo: Differential Geometry of Curves and Surfaces, Prentice-Hall, Inc. Englewood Cliffs, New Jersey 1976
[Fla] Fladt, Kuno: Analytische Geometrie spezieller ebener Kurven, Akademische Verlagsgesellschaft, Frankfurt am Main 1962
[Heu1] Heuser, Harro: Gewöhnliche Differentialgleichungen, B.G.Teubner, Stuttgart 1995
[Heu2] Heuser, Harro: Lehrbuch der Analysis 2, B.G.Teubner, Stuttgart-Leipzig-Wiesbaden 2000
[His] http://www-gap.dcs.st-and.ac.uk/~history/index.html
[Kor] Kordos, Marek: Streifzüge durch die Mathematikgeschichte, Ernst Klett Verlag, Stuttgart, Düsseldorf, Leipzig 1999
[Lex] Lexikon der Mathematik, Spektrum, Heidelberg 2001
[Pun] Eberhard Puntsch: Zitate Handbuch, Weltbild Verlag GmbH, Augsburg 1990
[Sch] Schupp, H; Dabrock, H: Höhere Kurven, B.I.-Wissenschaftsverlag, Mannheim-Leipzig-Wien-Zürich 1995
[Schw] Schwenk, Angela: Skript, 2000
[Ste] Stewart, Ian: Mathematik – Probleme, Themen, Fragen, Birkhäuser, Basel 1990
[Sto] Stoker, J.J.: Differential Geometry, Wiley-Interscience, New York-London-Sydney-Toronto 1989
Literatur zu I: Zykloide
[Kno] Knobloch, Eberhard: Abhandlungen der Akademie der Wissenschaften in Göttingen von Leibniz, Vandenhoeck & Ruprecht in Göttingen 1993
[Kon] Konforrowitsch, A.G.: Guten Tag, Herr Archimedes, Verlag Harry Deutsch, Frankfurt am Main und Thun 1996
[Pas] Pascal, Blaise: Zwei Abhandlungen über die Zykloide, gedruckt in der Nauck’schen Buchdruckerei, Berlin 1853
[Scr] Scriba, Christoph J.; Schreiber, Peter: 5000 Jahre Geometrie, Springer, Berlin-Heidelberg-New York 2002
[Tür] Türkheim, W.: Versuch einer populären Darstellung der Eigenschaften der Zykloide und ihrer Evolute, gedruckt bei Ludwig Heege, Schweidnitz 1840
Literatur zu II: Tautochrone
[Ort] Orthmann, C.: Das Problem der Tautochronen, Druck von U.W. Hahn’s Erben, Berlin 1872
Literatur zu III: Katakaustik
[Spa] Spallek, Karlheinz: Kurven und Karten, B.I.-Wissenschaftsverlag, Mannheim-Zürich-Wien 1980
Literatur zu IV: Brachistochrone
[Bol] Bolza, Oskar: Vorlesungen über Variationsrechnung, Chelsea Publishing Company, New York, N.Y.
[Fun] Funk, Paul: Variationsrechnung und ihre Anwendung in Physik und Technik, Springer Verlag, Berlin-Göttingen-Heidelberg 1962
[Gol] Goldstine, Herman H.: Die Streitschriften von Jacob und Johann Bernoulli, Birkhäuser Verlag, Basel-Boston-Berlin 1991
[Hüb] Hübner, Stefan: Johann Bernoulli und das Brachistochronenproblem
[Nat] Naturforschende Gesellschaft in Basel: Der Briefwechsel von Johann Bernoulli, Band 1, Birkhäuser Verlag 1991, Basel, Boston, Berlin
[Str] Struik, D.J.: A Source Book in Mathematics 1200 – 1800, Harvard University Press, Cambridge, Massachusetts 1969
[Wag] Wagner, Alfred: Die Variationsrechnung und ihre Basler Ursprünge Literatur zu V: Ausblick
[Ger] Gerthsen; Kneser; Vogel: Physik, Springer Verlag, Berlin-Heidelberg-New York 1977
[Gra] Gray, Alfred: Differentialgeometrie, Spektrum, Heidelberg-Berlin-Oxford 1994
Literatur zu VI: Biografische Notizen
[Kow] Kowalewski, Erhard: Große Mathematiker, J.F.Lehmanns Verlag, München-Berlin 1938
[Kra] Kraft, Fritz: Lexikon großer Naturwissenschaftler, Wiley-VCH 1999
[Mes] Meschkowski, Herbert: Denkweisen großer Mathematiker, Vieweg, Braunschweig 1990