Prof. Dr. Angela Schwenk

Das mathematische Pendel

Die Differentialgleichung für das mathematische Pendel lautet:
Dabei beschreibt y(t) den Ausschlag des Pendels zur Zeit t im Bogenmaß. w02 = g/l, wobei g die Erdbeschleunigung und l die Pendellänge ist.
Für kleine Winkel wird üblicherweise die Näherung sin(y)=y gemacht. Es ergibt sich damit als linearisierte Gleichung die klassische Schwingungsgleichung
In den folgenden Bildern sind die Lösungen von beiden Differentialgleichungen gegenübergestellt. Die Anfangsbedingungen entsprechen einem Anstoß des ruhenden Pendels. Die Anfangs(winkel)geschwindigkeit wird von Bild zu Bild vergrößert.
Es ist deutlich zu sehen, wie bei großen Auslenkungen (die Näherung sin(y)=y wird immer ungenauer ) die Lösungen immer mehr von einander abweichen.

Vergleich der Lösungen der Pendelgleichungen bei verschiedenen Anfangsgeschwindigkeiten:
rot :  Lösung der Gleichung   y '' + w02 sin(y) = 0 .
blau: Lösung der Gleichung  y '' + w02 y = 0 .

Daß die linearisierte Pendelgleichungen bei großen Auslenkungen physikalich unsinnige Lösungen hat, sieht man besonders deutlich an den folgenden Bildern, die die Pendelbewegungen darstellen. Das Pendelende bewegt sich auf einer Kreisbahn, damit die die einzelnen Ausschläge auseinandergehalten werden können, wurde die Pendellänge mit der Zeit t verkürzt gezeichnet.

Pendelbewegung zum ersten Bild oben (kleine Auslenkungen, Übereinstimmung von beiden Lösungen):

Pendelbewegung zum vierten Bild oben (große Auslenkungen, Abweichung der beiden Lösungen):

Pendelbewegung zum sechsten Bild oben (Das "echte " Pendel bleibt oben stehen und fällt dann zurück):

Pendelbewegung zum letzten Bild oben (Das "linearisierte" Pendel schlägt über und dann wieder zurück, das "echte" Pendel rotiert ständig aufgrund der hohen Anfangsgeschwindigkeit):

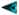<- Weitere Bilder

Letzte Änderung am: 03.07.97