zu den Aufgaben im Kapitel 6
Aufgabe 6.1: Beweisen Sie, dass ein Baum der Tiefe n (höchstens) 2n-1 Knoten besitzen kann. Oder anders herum: Ein Binärbaum mit n Knoten hat mindestens die Tiefe 1 + ëlog2 nû.
Lösung: Der Beweis erfolg nach dem Prinzip der mathematischen Induktion:
1. Die Aussage für n = 1 ist trivial: Ein Baum der Tiefe 1 hat genau 21-1 = 1 Knoten.
2. Angenommen, die Aussage stimmt für n. Wenn nun der Baum vertieft (nach unten verlängert) wird, können an jedem Knoten der untersten Stufe höchstens 2 weitere Knoten angehängt werden. Die Anzahl der Knoten der untersten Stufe ist (die Hälfte aller Knoten) höchstens 2n-1. Die Anzahl der neuen Knoten ist deswegen höchstens 2n. Wenn (nach der Annahme) die Anzahl der alten Knoten höchstens 2n-1 ist, dann ist die Anzahl aller Knoten höchstens 2n+2n-1 = 2n+1-1.
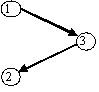
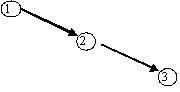
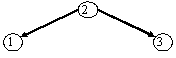
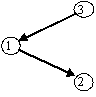
Aufgabe 6.2: Bilden Sie alle sortierten Binärbäume mit drei Knoten, die die Schlüssel 1, 2 und 3 haben.
Lösung:


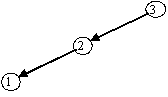
Aufgabe 6.3: Wie kann man die Anzahl der sortierten Binärbäume mit n Knoten (die die Schlüssel 1 bis n haben) berechnen?
Lösung: Sei long asb(long) die Funktion, die die Aufgabe löst. Offenbar muss gelten:
2.1. Induktionsanfang:
asb(0) == 1 (es gibt genau einen sortierten Baum mit 0 Knoten)
asb(1) == 1 (es gibt genau einen sortierten Baum mit einem Knoten)
2.2. Induktionsschritt: asb(n) == ?
Von den n Zahlen muss jeweils eine, nennen wir sie i, an der Wurzel stehen. Der linke Unterbaum der Wurzel enthält dann i-1 Knoten und der rechte Unterbaum der Wurzel enthält die übrigen n-1-i Knoten. Sortierte Bäume mit n Knoten und i an der Wurzel gibt es dann asb(i-1)*asb(n-1-i) viele („jeden linken Unterbaum kann man mit jedem rechten Unterbaum kombinieren“).
Wir müssen i von 1 bis n laufen lassen und all diese Zahlen addieren. Hier ist eine Java-Version der Funktion asb:
static long asb(long anzKnoten) { // Anzahl der sortierten Binärbäume if (anzKnoten < 0) return 0; if (anzKnoten <= 1) return 1; long erg = 0; for (long anzLinks = 0; anzLinks <= anzKnoten - 1; anzLinks++) { long anzRechts = anzKnoten - 1 - anzLinks; erg += (asb(anzLinks) * asb(anzRechts)); } return erg; }
Diese Funktion liefert folgende Ergebnisse (zum „Überprüfen von Hand“):
| n | asb(n) |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4 | 14 |
| 5 | 42 |
| 6 | 132 |
| 7 | 429 |
| 8 | 1430 |
| 9 | 4862 |
Aufgabe 6.4: Geben Sie einen Baum an, der zwar sortiert, aber nicht streng sortiert ist.
Lösung:

Die weiteren Lösungen fehlen noch