© APSIS GmbH ![]() , Polling,
2008
, Polling,
2008
Kapitel 10
Im Kapitel 7.5.5. haben wir die Zählerklasse für Verkehrszählung kennen gelernt. Wir erstellen jetzt eine ähnliche Klasse, die geeignet ist, fünf verschiedene Fahrzeugtypen (Motorrad, Pkw, Lkw, Bus, Sonstiges) getrennt zu zählen. Hierzu legen wir eine Reihung aus int-Werten als Klassenkomponente an:
class Verkehrszaehler { private final static int MOTORRAD = 0, PKW = 1, LKW = 2, BUS = 3, SONSTIGES = 4; private int[] zaehler = { 0, 0, 0, 0, 0 }; public void motorrad() { zaehler[MOTORRAD]++; } public void pkw() { zaehler[PKW]++; } … // usw., für lkw, bus und sonstiges ähnlich public void ergebnis() { System.out.println(zaehler[MOTORRAD] + "Motorräder"); System.out.println(zaehler[PKW] + "Pkws"); … } } // usw., für LKW, BUS und SONSTIGES ähnlich
Von dieser Klasse können nun für verschiedene Standorte mehrere Objekte ausgeprägt werden, ähnlich wie im Kapitel 7.5.5. Alternativ zum Reihungsliteral kann man einen Konstruktor schreiben:
public void Verkehrszaehler() {
zaehler = new int[5];
zaehler[MOTORRAD] = 0;
zaehler[PKW] = 0;
zaehler[LKW] = 0;
zaehler[BUS] = 0;
zaehler[SONSTIGES] = 0; }
In diesem Beispiel sehen wir die verbreitete Technik, in Java Aufzählungen zu programmieren: Die einzelnen Aufzählungswerte werden als final static int-Werte kodiert. Alternativ wäre es möglich, einen Aufzählungstyp
private enum Fahrzeug { MOTORRAD, PKW, LKW, BUS, SONSTIGES };
zu vereinbaren. Dann ist es aber nötig, bei jeder Verwendung eines Aufzählungswerts als Index etwa Fahrzeug.LKW.ordinal() zu schreiben.
Eine einfache sequenzielle Datei lässt sich damit leicht als polymorphe Klasse implementieren:
public class SeqDateiVektor implements SeqDatei { // hier ohne Ausnahmen private java.util.Vector inhalt = new java.util.Vector(); public void neuBeschreiben() { inhalt.removeAllElements(); } public void zuruecksetzen() { index = 0; } private int index = 0; public void eintragen(final Object element) { inhalt.addElement(element); } // wird ans Ende angehängt public void naechstesElement() { index ++; } public Object aktuellesElement() throws DateiendeException { try { return inhalt.elementAt(index); } // throws ArrayIndexOutOfBoundsException catch (ArrayIndexOutOfBoundsException ausnahme) { throw new DateiendeException(); } } public boolean endeDerDatei() { return index == inhalt.size(); } }
Die meisten Reihungen werden durch Zählschleifen bearbeitet, da die Anzahl ihrer Elemente am Anfang der Bearbeitung feststeht. Ein Beispiel dafür ist die Vektorrechnung. Unter einem Vektor versteht man in der Mathematik eine Zahlenreihe; meistens werden Vektoren als eindimensionale Reihungen implementiert. Vektoren kann man miteinander addieren, subtrahieren und multiplizieren. Unter der Summe zweier (gleichdimensionierter) Vektoren verstehen wir einen Vektor, dessen Elemente aus der Summe der entsprechenden Elemente beider Vektoren bestehen:
![]()
Abb.: Vektoraddition
Mathematisch kann dies folgendermaßen formuliert werden:
![]()
Die Addition eines Vektors zu sich selbst definiert die Multiplikation mit einer (ganzen oder Bruch-) Zahl:
![]()
Das Skalarprodukt zweier Vektoren mit gleichen Ausmaßen ist kein Vektor, sondern ein Objekt der Elementklasse. Es wird errechnet, indem je zwei Elemente der beiden Vektoren mit dem gleichen Index multipliziert und die Produkte addiert werden. Die mathematische Formel hierfür ist:
![]()
Die generische Klasse GVektor setzt eine Elementschnittstelle IElement mit den arithmetischen Methoden plus und mult voraus. Für die Implementierung der Schnittstelle ist dann eine Elementklasse nötig, die IElement erweitert. Darüber hinaus muss er den Null-Wert des Elements, das Produkt zweier Null-Vektoren (mit keinen Elementen, d.h. der Fall n = 0) exportieren. In der Implementierung des Vektors werden die oben erläuterten Algorithmen für Vektoroperationen mit Hilfe einer Reihung ausgeführt. Die Implementierung der arithmetischen Operationen läuft als Zählschleife über alle Elemente des Vektors. In der folgenden Klasse wurde plus als Mutator im Sinne von „dazuaddieren“ definiert (ähnlich wie += für arithmetische Typen):
interface IElement { public void plus(final IElement element); public void mult(final IElement element); public IElement zero(); } // liefert Nullelement der Klasse (z.B. 0 für Integer)
public class GVektor<Element implements IElement> { public IElement [] vektor; public GVektor(int laenge) { vektor = new Element[laenge]; }
public void plus(final GVektor that) throws UnpassendException { if (this.vektor.length != that.vektor.length) // vorbeugend throw new UnpassendException(); else for (int index = 0; index < vektor.length; index++) this.vektor[index].plus(that.vektor[index]); }
public void mult(final Element zahl) { … } // multipliziert mit zahl, ähnlich public Element mult(final GVektor that) throws UnpassendException { if (this.vektor.length != that.vektor.length) // vorbeugend throw new UnpassendException(); else { Element summe = that.vektor[0].zero(); // mit Nullwert vorbesetzen for (int index = 0; index < vektor.length; index++) { Element produkt = vektor[index]; produkt.mult(that.vektor[index]); summe.plus(produkt); } return summe; } }
public void kopieren(final GVektor that) throws VollException { try { if (this.vektor.length != that.vektor.length) { // ungleiche Größe vektor = new Element[that.vektor.length]; } // neu belegen; throws OutOfMemoryError for (int i = 0; i < vektor.length; i++) // elementweise kopieren this.vektor[i] = that.vektor[i]; } catch (OutOfMemoryError ausnahme) { throw new VollException(); } }
class UnpassendException extends Exception { } class VollException extends Exception { } }
In Java können für Klassen wie Element nur Methoden definiert werden, in anderen Sprachen (wie C++) aber auch Operatoren wie + und *. Dort kann die Zählschleife in der Methode mult einfacher geschrieben werden:
for (int index = 0; index < vektor.length; index++) summe += vektor[index] * v.vektor[index];
In Java wird diese Vorgehensweise verwendet, wenn die Elemente des Vektors keine Objekte, sondern arithmetische Variablen sind.
Bei der generischen Klasse GVektor gelten einige nichttriviale Entwurfsentscheidungen: Sie exportiert ihre Daten, d.h. die Reihung vektor ist nicht private, sondern public. Auf ihre Elemente kann der Benutzer nun direkt zugreifen: Er kann die Referenzen auf die gereihten Objekte mit Hilfe der Reihungsselektion [] lesen und beschreiben (d.h. die referenzierten Objekte erhalten bzw. neue Objekte eintragen). Dies ist beabsichtigt, weil er dadurch keinen inkonsistenten Zustand erzeugen kann.
Die Ausprägung dieser Klasse benötigt eine Elementklasse, für die die Methoden plus und mult zur Verfügung stehen. Diese sind in der Vektorklasse Rückrufmethoden, die beim Errechnen der Summe zweier Elemente aufgerufen werden:
class GanzElement implements IElement { private int wert; public GanzElement() { wert = 0; } public GanzElement(final int wert) { this.wert = wert; } public void plus(final IElement element) { GanzElement e = (GanzElement)element; wert += e.wert; } public void mult(final IElement element) { … // ähnlich public IElement zero() { return new GanzElement(0); } } …
GVektor<GanzElement> ganzVektor = new GVektor<GanzElement>(20); // Vektor für 20 Ganzzahlen ganzVektor.vektor[0] = new GanzElement(325); ganzVektor.vektor[1] = new GanzElement(-2315); … // usw., alle Vektorelemente werden besetzt ganzVektor.mult(new GanzElement(-1)); // Vorzeichen wird umgekehrt
Die generische Klasse GVektor kann natürlich für eine beliebige Elementklasse ausgeprägt werden, sofern geeignete Addition, Multiplikation und Nullelement für diese Klasse definiert wurden. Ein nicht allzu sinnvolles, aber funktionierendes Beispiel ist ein Vektor aus Eimern:
class EimerElement implements IElement { private Eimer wert; public EimerElement() { wert = new Eimer(); } public void plus(final IElement element) { … } // Summe zweier Eimer, wie auch immer sie errechnet wird public void mult(final IElement element) { … } // Produkt ähnlich public IElement zero() { … } // Nulleimer GVektor<EimerElement> eimerVektor = new GVektor<EimerElement>(5); // für fünf Eimer … // Eimer werden im Vektor abgelegt, addiert sowie ihr Skalarprodukt errechnet
Bemerkung: Ein Objekt der Standardklasse java.util.Vector (s. Kapitel 10.1.9) ist kein Vektor im obigen Sinne, vielmehr eine Reihung mit veränderbarer Länge.
Auch ein Sack (s. Kapitel 9.1.) mit diskreter Elementklasse kann als Reihung implementiert werden. Im Gegensatz zur Menge muss hier jedoch nicht nur über das Vorhandensein oder Fehlen einzelner Elemente Information gespeichert werden, sondern auch über ihre Anzahl. Von daher ist es notwendig, für den Elementtyp der Reihung statt boolean den Ganzzahltyp int zu nehmen:
class DiskreterSack<Element extends Enum> { implements IDiskreterSack<Element extends Enum> private int[] anzahl; public DiskreterSack(final int groesse) { anzahl = new int[groesse]; // für jeden Aufzählungswert ein int entleeren(); } // Sack ist zu Anfang leer public void entleeren() { // löscht alle Elemente aus dem Sack for (int i = 0; i < anzahl.length; i++) anzahl[i] = 0; } public void eintragen(final Element element) { anzahl[element.pos()] ++; } public void entfernen(final Element element) throws KeinEintragException { if (anzahl[element.pos()] == 0) throw new KeinEintragException(); else anzahl[element.pos()] --; } public void alleEntfernen(final Element element) { anzahl[element.pos()] = 0; } …
Geschachtelte Wiederholungen werden oft verwendet, um zweidimensionale Reihungen abzuarbeiten.
Ein zweidimensionaler Vektor heißt auch Matrix. Matrizen können auch miteinander addiert und multipliziert werden. Die Summe zweier Matrizen kann mit Hilfe einer geschachtelten Wiederholung errechnet werden:
public class GMatrix<Element implements IElement> { public IElement[][] matrix; public GMatrix(int breite, int hoehe) { matrix = new IElement[breite][hoehe]; }
public void plus(final GMatrix that) throws UnpassendException { // Summe if (this.matrix.length != that.matrix.length || this.matrix[0].length != that.matrix[0].length) throw new UnpassendException(); else { for (int zeile = 0; zeile < matrix.length; zeile++) for (int spalte = 0; spalte < matrix[0].length; spalte++) this.matrix[zeile][spalte].plus(that.matrix[zeile][spalte]); } }
public void mult(final Element zahl) { … } } // multipliziert mit zahl, ähnlich
Eine Assoziativtabelle (hash table) ist eine spezielle Implementierung eines Assoziativspeichers als Reihung. Die Elemente der Reihung sind Verbunde aus dem Schlüssel und dem Eintrag. Aus dem Schlüssel wird der Index des Eintrags in der Reihung mit Hilfe der Assoziativfunktion errechnet:
int hash (final schluessel); // const schluessel
Der hash-Wert modulo Tabellengröße (Operator %) ergibt den gesuchten Index. Ist z.B. der Schlüssel eine Zeichenkette, bildet die Summe der ASCII-Werte der Zeichen eine zwar nicht optimale, aber doch geeignete Assoziativfunktion.
Durch die Methode eintragen wird ein neues Element in die Tabelle eingetragen. Mit ihm zusammen wird auch ein Schlüssel (z.B. eine Zeichenkette) angegeben. Die Assoziativfunktion wird auf- (besser: zurück-) gerufen, um aus dem Schlüssel einen Tabellenindex (z.B. ASCII-Summe modulo Tabellengröße) zu errechnen. An diesem Index wird i.A. das neue Element (zusammen mit dem Schlüssel) eingetragen. Es kann natürlich vorkommen, dass dieser Platz in der Tabelle schon belegt ist, weil ein anderer Index zufällig denselben Hash-Wert ergeben hat. In diesem Fall wird der nächste freie Platz in der Tabelle gesucht (zyklisch, d.h. dem letzten Index folgt der erste); wenn keiner mehr gefunden wird, ist sie voll.
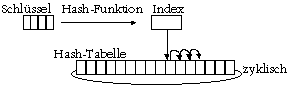
Abb.: Assoziativtabelle
Die Methode finden ruft die Assoziativfunktion ebenfalls auf, um aus dem Parameter-Schlüssel einen Tabellenindex zu errechnen. Von diesem Index an wird der Schlüssel (bis zum nächsten freien Platz) gesucht. Wenn er gefunden wurde, wird das mit ihm gespeicherte Element zurückgegeben; wenn nicht, wird eine Ausnahme ausgelöst. Um dieser Ausnahme vorzubeugen, kann die Methode vorhanden zuvor aufgerufen werden. Damit der Index hierbei nicht wiederholt errechnet werden muss (vielleicht ist die Assoziativfunktion sehr aufwändig), sollte sich die Klasse (oder das Objekt) ihn intern merken.
Wenn die Assoziativtabelle nicht allzu voll ist, findet sie sehr schnell (in 1-3 Schritten) den gesuchten Eintrag. Je voller sie ist, desto langsamer wird sie; wenn sie fast voll ist, muss u.U. die ganze Tabelle durchsucht werden. Um dem Benutzer die Information zur Verfügung zu stellen, wie effektiv seine Assoziativtabelle ist, wird die Gesamtzahl der Verschiebungen durch einen Informator
int verschiebungen();
zur Verfügung gestellt. Zu Anfang ist dieser Wert 0; jede Eintragung, die den nächsten freien Platz sucht, erhöht den Wert um die Anzahl der notwendigen Schritte.
Methoden wie kopieren und istGleich werden normalerweise mit Hilfe einer Wiederholung implementiert – ähnlich wie im Kapitel 11.1.5. die Methode textSpeichern. Die im Kapitel 3.3.8. schon vorgestellte Technik der Rekursion ist jedoch auch geeignet, alle Elemente einer verketteten Liste abzuarbeiten:
public void kopieren(final IStapel that) throws VollException { anker = knotenKopie((StapelL)that.anker); }
private static Knoten knotenKopie(final Knoten qu) throws VollException { try { Knoten ziel = new Knoten(qu.wert); // throws NullPointerException bei qu == null ziel.verbindung = knotenKopie(qu.verbindung); // rekursiver Aufruf return ziel; } catch (NullPointerException ausnahme) { return null; } // Liste zu Ende catch (OutOfMemoryError ausnahme) { // kein Speicher mehr frei throw VollException; } }
public boolean istGleich(final IStapel that) { // const return knotenVergleich(anker, (StapelL)that.anker); }
private static boolean knotenVergleich(final Knoten erster, final Knoten zweiter) { try { return erster.wert == zweiter.wert && // throws NullPointerException, wenn eine Referenz == null knotenVergleich(erster.verbindung, zweiter.verbindung); } catch (NullPointerException ausnahme) { // eine der Listen zu Ende return erster == zweiter; } } // ob auch die andere?
Die privaten Methoden können hier als Klassenmethoden (mit static) vereinbart werden, da sie nicht am Zielobjekt (StapelL), sondern nur an ihren Parametern arbeiten. In knotenVergleich ist es sinnvoll, die kurzgeschlossene Konjunktion zu verwenden, damit bei Ungleichheit der Werte keine weiteren rekursiven Aufrufe stattfinden.
Die Unterbrechung der Rekursion geschieht hier mit der vom Interpreter ausgelösten Ausnahme NullPointerException: Der Versuch scheitert, am Ende der Liste ein Objekt über eine null-Referenz zu erreichen.
Im Kapitel 3.3.6. haben wir den Stapelungsmechanismus für Aufrufe schon vorgestellt. Bei den rekursiven Aufrufen, wie z.B. von knotenKopie, wird dieser Mechanismus voll ausgenutzt. Am Beispiel einer verketteten Liste aus drei Elementen kann dies einleuchtend untersucht werden.
Nehmen wir an, für ein Objekt Namens a der Klasse Stapel ist die Methode eintragen dreimal mit den Parametern '1', '2', und '3' aufgerufen worden. Hiernach entsteht eine verkettete Liste aus drei Gliedern, die wir mit 1, 2 und 3 nummerieren:

Abb. Rekursive Abarbeitung
Ein anschließender Aufruf von
b.kopieren(a);
wird auf dem Stapel in folgenden Schritten abgearbeitet:

Abb.: Stapel bei Rekursion
1. Im Stapelbereich der Methode, die diesen Aufruf enthält, befindet sich je eine Referenz a (zeigt auf das StapelL-Objekt mit der Komponente anker, wie in der 10.8 dargestellt) und b (zeigt auf ein anderes StapelL-Objekt, das jetzt mit der Kopie überschrieben werden soll).
2. Für kopieren wird auf dem Stapel ein neuer Bereich angelegt. Hier wird die Parameterreferenz quelle gespeichert. Weil der aktuelle Parameter des Aufrufs a ist, wird der Inhalt von a in quelle kopiert; quelle zeigt somit auch auf das in der 10.8 dargestellte StapelL-Objekt.
3. Als einzige Anweisung von kopieren wird Zuweisung anker = knotenKopie() mit dem Parameter quelle.anker aufgerufen. Die linke Seite der Zuweisung anker ist dabei die Komponente des Zielobjekts b des kopieren-Aufrufs, d.h. b.anker wird mit dem Ergebnis des Funktionsaufrufs überschrieben werden (nach der Rückkehr aus der Funktion).
4. Für knotenKopie wird am Stapel ein neuer Bereich angelegt. Hier bekommt die Parameterreferenz qu ihren Platz. Weil der aktuelle Parameter des Aufrufs quelle.anker, d.h. a.anker ist, zeigt jetzt qu auf das Objekt Nr. 3 in der 10.8.
5. Als erste Anweisung von knotenKopie wird in seinem Stapelbereich eine lokale Referenz ziel vom Typ Knoten angelegt.
6. Anschließend wird der Erzeugeroperator new Knoten ausgeführt. Prinzipiell kann hier wegen Speichermangel (mit geringer Wahrscheinlichkeit) OutOfMemoryError ausgelöst werden; dies wird aufgefangen und der Aufruf von kopieren mit VollException abgebrochen. In diesem Fall behält b.anker seinen ursprünglichen Wert, d.h. das Kopieren findet nicht statt.
7. Wenn das neue Knoten-Objekt erfolgreich erzeugt werden kann, wird es auf der Halde als Objekt Nr. 4 gleichzeitig mit dem Wert {qu.wert, null} vorbesetzt. Die Referenz qu zeigt auf das oben dargestellte Objekt Nr. 3, seine wert-Komponente (mit dem Inhalt '3') wird also in das neu erzeugte Objekt kopiert. Die lokale Referenz ziel verweist jetzt auf das Objekt Nr. 4.
8. In die verbindung-Komponente des Objekts Nr. 4 soll nun das Ergebnis des zweiten (rekursiven) Aufrufs von knotenKopie geschrieben werden.
9. Hierzu wird ein neuer Stapelbereich angelegt. Für die Parameterreferenz qu (ein zweites Exemplar) wird Platz reserviert. Hierin wird der Wert des aktuellen Parameters qu.verbindung (des ersten qu-Exemplars) hineinkopiert. Da das erste qu auf das Objekt Nr. 3 verweist, zeigt qu.verbindung auf das Objekt Nr. 2 qu (das zweite Exemplar) verweist ebenso auf das Objekt Nr. 2.
10. Die Aktionen ab dem 5. Schritt werden erneut ausgeführt: ziel wird im neuen Stapelbereich angelegt und ein neuer Knoten Nr. 5 wird erzeugt. Seine wert-Komponente (d.h. '2') wird ins qu.wert kopiert.
11. In die verbindung-Komponente des Objekts Nr. 5 soll wieder das Ergebnis des rekursiven, schon des dritten Aufrufs von knotenKopie geschrieben werden.
12. Im neuen Stapelbereich (für den dritten Aufruf von knotenKopie) entsteht das dritte Exemplar von qu, in die qu.verbindung (vom zweiten Exemplar) – ein Verweis auf das Objekt Nr. 1 – kopiert wird.
13. In der dritten Ausführung von knotenKopie entsteht ein drittes Exemplar von ziel; sie verweist auf das neu erzeugte Objekt Nr. 6. Hierin wird qu.wert aus dem Objekt Nr. 1 hineinkopiert, d.h. '1'.
14. Die verbindung-Komponente des Objekts Nr. 6 soll nun mit dem Ergebnis eines vierten Aufrufs von knotenKopie besetzt werden.
15. Hierfür wird ein neuer Stapelbereich mit dem vierten qu angelegt; sie wird mit qu.verbindung besetzt. Da qu (das dritte Exemplar) auf das Objekt Nr. 1 verweist, erhält qu (der vierte) den Wert null.
16. Ein weiterer Knoten wird nun erzeugt. Der Versuch des Konstruktors, seine wert-Komponente mit qu.wert zu besetzten, löst diesmal eine NullPointerException aus, da qu == null. Sie wird aufgefangen und return null; im catch-Block wird ausgeführt: Der vierte Aufruf von knotenKopie kehrt mit dem Ergebnis null zur aufrufenden Stelle (in den dritten Aufruf) zurück.
17. Dieses Ergebnis null wird in ziel.verbindung (in die verbindung-Komponente des Objekts Nr. 6) geschrieben.
18. Anschließend wird die return-Anweisung des dritten Aufrufs ausgeführt. Sein Ergebnis ist ziel (die dritte), d.h. das Objekt Nr. 6. Die Steuerung kehrt in den zweiten Aufruf zurück.
19. Dieses Ergebnis wird in ziel.verbindung (in die verbindung-Komponente des Objekts Nr. 5) geschrieben: Das Objekt Nr. 5 wird zum Objekt Nr. 6 verkettet.
20. Anschließend wird die return-Anweisung des zweiten knotenKopie-Aufrufs ausgeführt. Sein Ergebnis ist ziel (der zweite), d.h. das Objekt Nr. 5. Die Steuerung kehrt in den ersten Aufruf zurück.
21. Der Verweis auf das Objekt Nr. 5 wird in ziel.verbindung (in die verbindung-Komponente des Objekts Nr. 4) geschrieben: Das Objekt Nr. 4 wird zum Objekt Nr. 5 verkettet.
20. Die return-Anweisung des ersten knotenKopie-Aufrufs ausgeführt. Sein Ergebnis ist ziel, d.h. ein Verweis auf das Objekt Nr. 4. Die Steuerung kehrt in den Aufruf von kopieren zurück.
21. Das Ergebnis (Objekt Nr. 4) wird in anker (des Objekts b) geschrieben. Der Aufruf von kopieren ist nun abgeschlossen.
Die Technik der rekursiven Abarbeitung einer Liste ist sicherlich nicht die effektivste, da das Anlegen und das Löschen der Stapeleinträge mit Aufwand verbunden ist (s. Kapitel 3.3.9.). Beim Kopieren einer langen Liste kann hierbei der Stapel überlaufen. Die Lösung mit einer Wiederholung ist von diesen Schwächen frei. Nichtsdestotrotz gibt es Situationen, wo ein rekursiver Algorithmus einfacher, daher lesbarer ist als eine Wiederholung (s. z.B. Kapitel 8.4.2.).
Eine einfache Verwendung von Reihungen ist die Übersetzungstabelle. Mit Hilfe von zwei Tabellen kann eine Entsprechung (d.h. eine Eins-zu-eins-Abbildung) zwischen Werten hergestellt werden. Ein Beispiel sei die Übersetzung der eigenen Farben in die Farben der Standardklasse java.awt.Color, die in Grafik-Methoden von Standardklassen verwendet werden:
import java.awt.Color; class Farbe extends lehrbuch.Aufz { public static final Farbe GRUEN = new Farbe(); public static final Farbe LILA = new Farbe(); ... } // usw. public class Farbuebersetzer { private static final Color [] rgb = { Color.green, Color.magenta, ... }; // in der Reihenfolge, wie die deutschen Farbnamen in Farbe vereinbart wurden public static Color farbuebersetzer (final Farbe farbe) { return rgb [farbe.pos()]; } }
Der Benutzer dieser Klasse kann nun eine eigene Farbe in die entsprechende Standardfarbe übersetzen:
getGraphics().setColor (Farbuebersetzer.farbuebersetzer(Farbe.LILA));
Die Funktion farbuebersetzer greift auf die klasseninterne konstante Reihung rgb zu, in der die benötigten Standardfarben den eigenen Farben entsprechend aufgelistet sind. Der Zugriff auf ein Element dieser Reihung erfolgt mit einem Indexwert, der von der Aufzählungsmethode pos der Farbe geliefert wird.
Übung: Programmieren Sie dem Farbübersetzer mit der Technik aus dem Programm (10.4), Aufzählungen als final static int-Werte zu kodieren.
Übung: Schreiben Sie ein Java-Applet, in dem – ähnlich wie im Programm (3.11) – eine Schriftzeile ausgegeben wird, deren Farbe aber zuvor von einer Auswahlliste (auswahl aus lehrbuch.Farbe oder getSelectedItem aus java.awt.Choice) ausgewählt wird.
Die Implementierung des Stapels benutzt eine rückwärts verkettete Liste, die der Warteschlange eine vorwärts verkettete Liste. Die geeignete Technik wird je nachdem gewählt, in welche Richtung entlang der Liste gewandert werden muss. Wenn von einem Knoten beide seiner Nachbarn erreicht werden müssen, wird eine doppelt verkettete Liste verwendet. Seine Knoten enthalten nicht nur einen, sondern zwei Verweise:
class Knoten<Element> { Element wert; Knoten vorwaerts, rueckwaerts; } // Vor- und Rückwärtsverkettung
Die Schnittstelle PosListe kann mit dieser Technik nach vorne und nach implementiert werden. Die Listenobjekte enthalten diesmal drei Anker: Sie verweisen auf den ersten und den letzten Knoten der Liste sowie auf das aktuelle Element:
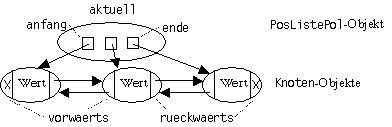
Abb.: Doppelt verkettete Liste
Durch jede Methode wird der von aktuell referierte Knoten (und evtl. ihre Nachbarn) manipuliert. Die Anker anfang und ende werden nur in den Methoden anfang und ende gebraucht, um aktuell geeignet positionieren zu können:
public class GListe<Element> implements IListe { // generische Implementierung als doppelt verkettete Liste private class Knoten<Element> { Object wert; Knoten vorwaerts, rueckwaerts; // Vor- und Rückwärtsverkettung Knoten(Object wert, Knoten vorwaerts, Knoten rueckwaerts) { wert = wert; vorwaerts = vorwaerts; rueckwaerts = rueckwaerts; } } private Knoten anfang, ende, aktuell; public GListe() { entleeren(); } public void entleeren() { // macht die Liste leer anfang = null; ende = null; aktuell = null; } public void eintragen(final Element element) throws VollException { // trägt element hinter die aktuelle Position ein try { ... // hier nur der allgemeine Fall mitten in der Kette: Knoten neu = new Knoten(element, aktuell.vorwaerts, aktuell); // neuer Knoten zeigt vorwärts auf den aktuellen, rückwärts auf den dahinter aktuell.vorwaerts.rueckwaerts = neu; // nach dem aktuellen einfügen aktuell.vorwaerts = neu; aktuell = neu; } catch (OutOfMemoryError ausnahme) { throw vollException; } } public void erstesEintragen(final Element Element) { ... // ähnlich public void loeschen() throws LeerException { try { ... // hier nur der allgemeine Fall mitten in der Kette: Knoten hinten = aktuell.rueckwaerts; // throws NullPointerException, wenn Liste leer: aktuell = null Knoten vorne = aktuell.vorwaerts; // throws NullPointerException, wenn Liste leer hinten.vorwaerts = vorne; vorne.rueckwaerts = hinten; aktuell = hinten; } catch (NullPointerException ausnahme) { throw leerException; } } public Element aktuellesElement() throws LeerException { try { return aktuell.wert; } // throws NullPointerException catch (NullPointerException ausnahme) { throw leerException; } } public void vorwaerts() throws LeerException { try { aktuell = aktuell.vorwaerts; } catch (NullPointerException ausnahme) { throw leerException; } } public void rueckwaerts() throws LeerException { ... // ähnlich public void anfang() { aktuell = anfang; } public void ende() { aktuell = ende; } public boolean istLeer(){ return anfang == null; } ... } // weitere Methoden
Die auch rekursiv implementierbaren Methoden speichern, laden, kopieren, istGleich und suchen werden wir im Kapitel 10.3.7. mit Hilfe einer Wiederholung programmieren.
Übung: Programmieren Sie die Methoden kopieren, istGleich und suchen der positionierbaren Liste mit Hilfe der Ausprägung des iterators.
Wir haben oben Knoten mit zwei Referenzen benutzt, um eine doppelt verkettete Liste zu programmieren. Eine ähnliche häufige Datenstruktur, für die man Knoten mit zwei Referenzen benötigt, ist der Binärbaum:
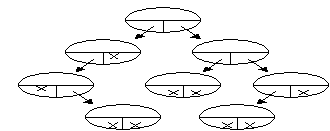
Abb.: Binärbaum
Im Binärbaum wird jeder Knoten (außer dem obersten Wurzelknoten) genau einmal referiert und jeder Knoten referiert höchstens zwei andere Knoten, seine Nachfolger.
Ein Binärbaum kann auf drei typische Arten durchsucht (durchwandert oder traversiert ) werden. Diese drei Arten werden wir mit den englischen Bezeichnungen Präorder, Inorder und Postorder nennen. Bei der Präorder-Traversierung wird die Wurzel vor den beiden Teilbäumen bearbeitet. Beim Inorder-Durchsuchen wird die Wurzel zwischen den beiden Teilbäumen manipuliert, bei Postorder wird die notwendige Operation zuerst an den beiden Teilbäumen, anschließend an der Wurzel durchgeführt. Diese drei Vorgehensweisen können in Iteratoren programmiert werden.
Die Operationen am Binärbaum werden einer Schnittstelle festgelegt:
public interface Binaerbaum { public void eintragen(final Object element); // trägt element in den Baum ein // ensures vorhanden(element); public boolean vorhanden(final Object element); // const public Object spitze(); // const // Wurzelelement des Baums public void iteratorPre(); // Präorder public void iteratorIn(); // Inorder public void iteratorPost(); } // Postorder
Zur Programmierung der Iteratoren ist es nötig, für die Elemente die durchzuführenden Operationen in einer Schnittstelle zu definieren:
interface Element { public void rueckruf(); } // die im Iterator durchzuführende Operation public class BaumKnoten implements Binaerbaum { private Element wert; private BaumKnoten links, rechts; public BaumKnoten(final Element wert, final BaumKnoten links, final BaumKnoten rechts) { ' this.wert = wert; this.links = links; this.rechts = rechts; } public Object spitze() { return wert; } public boolean vorhanden(final Object element) { return wert.equals(element) || // kurzgeschlossene Disjunktionen (links != null && links.vorhanden(element)) || (rechts != null && rechts.vorhanden(element)); } public void iteratorIn() { try { links.iteratorIn(); } // linken Teilbaum bearbeiten catch (NullPointerException a) { } // links == null, kein linker Teilbaum wert.rueckruf(); // Knoten bearbeiten try { rechts.iteratorIn(); } // rechten Teilbaum bearbeiten catch (NullPointerException a) { } } // rechts == null, kein rechter Teilbaum ... // andere Iteratoren ähnlich: wert.rueckruf jeweils vor bzw. nach den Teilbäumen }
In dieser Klasse haben wir keinen Unterschied zwischen einem Knoten und einem Baum gemacht. Diese Technik ist zwar einfach, hat aber den Nachteil, dass es keinen „leeren Baum“ gibt. Wenn die Baum-Klasse eine Referenz wurzel auf ein Knoten-Objekt enthält (ähnlich wie unsere bisherigen Multibehälter), dann kann auch der leere Baum (mit wurzel == null) dargestellt werden. Andere Baum-Darstellungen werden in [SolAlg] erörtert.
Im Kapitel 3.3.8. haben wir eine Ausnahme für den Abbruch einer Rekursion benutzt. In der Praxis wird hierzu oft eine Alternative (mit if) benutzt.
Als Beispiel betrachten wir jetzt eine Implementierung der Schnittstelle Binaerbaum, die wir im Kapitel 10.3.8. kennen gelernt haben.
Ein Binärbaum heißt sortiert, wenn für jeden Knoten gilt: Der Wert jedes Elements im linken Zweig ist nicht größer als der Wert des aktuellen Knotens und der Wert jedes Elements im rechten Zweig ist nicht kleiner als der Wert des aktuellen Knotens. Um Elemente in einen sortierten Binärbaum eintragen zu können, ist es nötig, dass die Elementklasse eine geeignete (Rückruf-) Methode für den Wertevergleich definiert:
interface SortElement extends Element { public boolean istKleiner(final SortElement element); } // vergleicht zwei Elemente // requires a.istKleiner(b) | b.istKleiner(a) | a.istGleich(b); public class SortierterBinaerbaum extends BaumKnoten implements Binaerbaum { public void eintragen(SortElement element) { if (element.istKleiner((SortElement)wert)) { // Element-Rückruf if (links == null) links = new SortierterBinaerbaum(element); // neuer Baum else links.eintragen(element); } // Rekursion else { ... } // rechts ähnlich // vorhanden kann mit SortElement schneller laufen, deswegen wird sie überschreiben: public boolean vorhanden(final SortElement element) { if (element.istKleiner((SortElement)wert)) return links == null || links.vorhanden(element); // Rekursion else if (((SortElement)wert).istKleiner(element)) return rechts == null || rechts.vorhanden(element); // Rekursion else // wert.istGleich(element) return true; } }
An den gekennzeichneten Stellen sieht man, dass der rekursive Aufruf bedingt erfolgt, d.h. nur wenn eine Bedingung erfüllt ist: In allen Fällen endet die Rekursion an einem leeren Teilbaum. Statt der hier benutzten Steuerkonstrukte kann dieser Fall auch durch Auslösen der Ausnahme NullPointerException erkannt werden.
Damit ist jedoch noch nicht gewährleistet, dass die Rekursion tatsächlich endet, dass die Abbruchbedingung erreicht wird. Dazu ist zusätzlich erforderlich, dass bei jedem Aufruf ein – im Sinne des Abbruchkriteriums „kleineres“ – Objekt überprüft wird: Typischerweise ist dies das Zielobjekt oder ein Parameter, seltener ein globales Objekt. Im obigen Beispiel erkennt man leicht, dass jeder rekursiver Aufruf mit einem reduzierten Zielobjekt erfolgt, sodass das Kriterium „leerer Teilbaum“ erreicht werden muss. Ein Programmierfehler (z.B. Zyklus im Baum) kann dabei böse Überraschungen (endlose Rekursion) zu Folge haben.
Hier wurde also vor dem rekursiven Aufruf (in den gekennzeichneten Zeilen) jeweils eine Bedingung überprüft, ob die Rekursion fortgesetzt werden soll.
Die aufgeschobene Klasse lehrbuch.Aufz wurde als eine mehrfach verkettete Liste implementiert. Ihre Unterklasse lehrbuch.Farbe hat z.B. folgende Struktur:
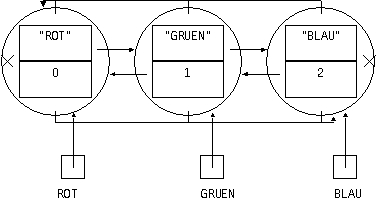
Abb.: Aufzählungsklasse Farbe
Für jede neue Aufzählungsklasse wird eine eigene mehrfach verkettete Liste erzeugt. Die Aufzählungsobjekte, die je einen Aufzählungswert repräsentieren, werden in der Unterklasse mit Hilfe des geschützten (parameterlosen) Konstruktors – z.B. in new Farbe() – erzeugt. Dabei stellt der Konstruktor die Verkettung der Aufzählungsobjekte her. Ein Aufzählungsobjekt (z.B. GRUEN) wird als ein Knoten innerhalb einer Aufz-Unterklasse (z.B. Farbe) implementiert, der neben den zwei Datenfeldern (Name als String und Position als int) vier Verweise hat: zum Vorgänger, zum Nachfolger sowie zum ersten und zum letzten Knoten:
protected final class Knoten implements java.io.Serializable { String bild; // Name des Wertobjekts int pos; // Position (Anfang bei 0) Aufz naechster,vorheriger,erster,letzter; } // verkettete Liste innerhalb eines Typs // vorheriger soll nicht für den ersten Knoten referiert werden // naechster soll nicht für den letzten Knoten referiert werden private Knoten knoten; private static Aufz ersterAkt, letzterAkt; // Randknoten für den aktuellen Typ protected Aufz() { // geschützter Konstruktor; soll nur für die Erzeugung // eines neuen Aufzählungswerts innerhalb eines Typs aufgerufen werden knoten = new Knoten(); if (letzterAkt == null || letzterAkt.getClass() != getClass()) { // neuer Typ knoten.pos = 0; ersterAkt = this; letzterAkt = this; } // neuer letzter Wert für den aktuellen Typ // vorheriger == null für den ersten Wert, naechster == null für den letzten Wert else { // neuer Wert für denselben Typ, verketten: knoten.pos = letzterAkt.knoten.pos + 1; knoten.vorheriger = letzterAkt; letzterAkt.knoten.naechster = this; letzterAkt = this; } // neuer letzter Wert für den aktuellen Typ
knoten.bild = getClass().getFields()[knoten.pos].getName(); // siehe Kapitel 10.4.2. knoten.erster = ersterAkt; // erster Wert für den aktuellen Typ // setzen letzter-Komponente auf letzterAkt in allen Knoten für den aktuellen Typ: Aufz ref = ersterAkt; for (int i = 0; i <= knoten.pos; i++) { ref.knoten.letzter = letzterAkt; ref = ref.knoten.naechster; } }
Der geschützte Konstruktor Aufz wird in der Vereinbarung einer Aufzählungsklasse für die Definition eines neuen Aufzählungswerts aufgerufen:
public static final Farbe GRUEN = new Farbe();
Hierbei wird ein neuer Knoten erzeugt, der mit den anderen Wertknoten verkettet wird, um innerhalb des Aufzählungstyps navigieren zu können. In der letzten Zeile wird der Name des Aufzählungswerts (z.B. "GRUEN") als String ermittelt und in der Komponente name gespeichert. Wie dies möglich ist, werden wir im Kapitel 10.4.2. studieren.
© APSIS GmbH ![]() , Polling,
2008
, Polling,
2008