© APSIS GmbH , Polling, 2008

Kapitel 8

Erkennen einer Ausnahmesituation

Ein Beispiel hierfür ist in der Implementierung der Aufzählungsmethode naechster aus dem Programm (7.1), die eine Ausnahme werfen soll:

public Gefuellt naechster() throws Ausnahme {
  if (this == NEIN)
   throw new Ausnahme();
  else
   return NEIN;
}

public Gefuellt vorheriger() throws Ausnahme { 
  if (this == JA)
   throw new Ausnahme();
  else
   return JA;
}

Verwendung der Schleifenarten

In den vergangenen Kapiteln haben wir alle Schleifenarten kennen gelernt, die in verschiedenen Programmiersprachen angeboten werden. Sie können folgendermaßen zusammengefasst werden:

• rumpfgesteuerte Schleife
• fußgesteuerte Schleife
• kopfgesteuerte Schleife
  • Zählschleife
    • Festschleife

Hiernach sind die fuß- und die kopfgesteuerte Schleife jeweils ein Sonderfall der rumpfgesteuerten Schleife: der zweite bzw. der erste Block sind jeweils leer.

Die Zählschleife ist ein Sonderfall der kopfgesteuerten Schleife, da hier die Anzahl der Wiederholungen beim Eintritt in die Schleife feststeht. Die Festschleife ist ein Sonderfall der Zählschleife, da hier die Anzahl der Wiederholungen schon zur Übersetzungszeit bekannt ist.

Aus den grundlegenden Eigenschaften der Schleifen ergeben sich ihre typischen Einsatzgebiete: Endliche Zählschleifen werden überwiegend zur Abarbeitung von Reihungen (deren Größe feststeht, s. Kapitel 10.1.) verwendet, während Dateien und dynamische Datenstrukturen (die ihre Größe zur Laufzeit ändern können, s. Kapitel 10.3.) mit vor- und nachprüfenden Schleifen durchwandert werden:

while (! eingabeDatei.ende()) { 
   element = eingabeDatei.lesen();
   element.bearbeiten();
   ausgabeDatei.schreiben(element); }

oder

referenz = anker; // verkettete Liste, s. Kapitel 10.3. 
while (referenz != null) {
   referenz.wert.bearbeiten();
   referenz = referenz.verbindung; }

Nachprüfende Schleifen bieten sich dabei an, wenn die Datenstruktur mit Sicherheit mindestens ein Element enthält:

do {
   element = eingabeDatei.lesen(); }
   element.bearbeiten();
while (! eingabeDatei.ende());

Oft werden Daten in einer Schleife gelesen. Dies ist ein Fall für die rumpfgesteuerte Schleife: Die Daten werden im ersten Block eingelesen. Wenn hierbei das Endekriterium erkannt wird (Daten mit hierfür spezifischem Inhalt), wird die Schleife (mitten im Rumpf) abgebrochen – der erste Block wird nicht (mehr) ausgeführt.

while (true) {
   element = eingabeDatei.lesen(); // z.B. Zahl von der Konsole
if (element.endekriterium()) break; // z.B. Zahl ist 0
   element.bearbeiten(); } // z.B. aufaddieren

Gleichwertigkeit von Wiederholungen

Die Verfügbarkeit von syntaktischen Konstruktionen für die verschiedenen Schleifenarten stellt keine Einschränkung für den Programmierer dar, da alle Schleifenarten durch ein Endlosschleifenkonstrukt ausgedrückt werden können (nicht dagegen durch – endliche – Zählschleifen).

Die rumpfgesteuerte Schleife kann beispielsweise durch die kopfgesteuerte Schleife folgendermaßen simuliert werden. Der Preis dafür ist entweder die Verdopplung eines Blocks oder die Einführung einer Booleschen Steuervariablen: Der Abschnitt

while (true) {
   … // erster Block
if (abbruchbedingungErfuellt) break;
   … // zweiter Block
}

bewirkt dasselbe wie der Abschnitt

… // erster Block verdoppelt
while (! abbruchbedingungErfuellt) {
   … // zweiter Block
   … // erster Block
}

oder der Abschnitt mit einer zusätzlichen Steuervariablen:

boolean weiter = true;
while (weiter) {
      … // erster Block
   weiter = ! abbruchbedingungErfuellt;
   if(weiter)
   … // zweiter Block
}

Die rumpfgesteuerte Schleife kann selbstverständlich die kopf- und die fußgesteuerte Schleife ersetzten, da diese nur Sonderfälle der ersten sind. Die Zählschleife ist ein Spezialfall der kopfgesteuerten Schleife, somit kann sie durch eine geeignet formulierte ersetzt werden:

for (int i = anfang; i <= ende; i++) 
   … // Rumpf

ist gleichwertig mit

int i = anfang;
while (i <= ende) {
   … // Rumpf
   i++; }

Umgekehrt gilt die Ersetzbarkeit jedoch nicht: Durch Zählschleifen können nicht alle anderen Wiederholungen ersetzt werden. Der Unterschied liegt in der wesentlichen Eigenschaft der Zählschleife: Beim Eingang in die Wiederholung steht die Anzahl der Durchläufe fest. Eine Zählschleife kann nie endlos laufen. Für die anderen Schleifenarten gilt diese Aussage nicht, deswegen kann die Zählschleife nicht andere ersetzen.

Die Türme von Hanoi

Ein drittes Standardbeispiel für rekursive Algorithmen ist die Lösung des Kinderspiels, das unter dem Namen Türme von Hanoi bekannt ist. Hier muss eine gegebene Anzahl von gestapelten Ringen unterschiedlicher Größe von einer Stange auf eine andere mit Hilfe einer Dritten übertragen werden. Hierbei darf ein größerer Ring nie auf einen kleineren gelegt werden:

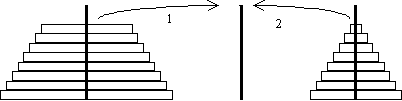
Abb.: Türme von Hanoi

Es gibt eine einfache, einleuchtende rekursive und eine komplizierte iterative Lösung. Die Zeitkomplexität beider Algorithmen ist jedoch O(2n), der Vorteil des iterativen Algorithmus liegt nur in seiner konstanten Speicherkomplexität (gegenüber der logarithmischen):

void uebertragen(int n, final String a, final String b, final String c) { 
      // überträgt n Scheiben von a nach b mit Hilfe von c
   if (n > 0) {
        uebertragen(n-1, a, c, b);
      System.out.println("Übertragung von " + a + " nach " + b);
        uebertragen(n-1, c, b, a); } }
void hanoi(int anzahl) {
   uebertragen(anzahl, "ersten", "zweiten", "dritten"); }

Die Idee für diese rekursive Lösung ist wieder das Prinzip der mathematischen Induktion (s. auch Übung 10.3). Wir nennen den (trivialen) Algorithmus für die Übertragung der kleinsten Scheibe von einer Stange auf eine andere A₁. Die zwei kleinsten Scheiben werden mit A₂ übertragen usw. Wenn wir nun die n (kleinsten, oberen) Scheiben von einer Stange zur anderen mit einem Algorithmus A_n übertragen können, dann können wir n+1 Scheiben folgendermaßen übertragen. Zuerst übertragen wir die oberen n Scheiben mit dem Algorithmus A_n von der ersten Stange auf die zweite, dann übertragen wir die n+1-te (größte) Scheibe von der ersten auf die dritte Stange (die keine Scheibe enthält), und dann verwenden wir wieder den Algorithmus A_n, um die oberen n Scheiben von der zweiten auf die dritte Stange zu übertragen. Als Ergebnis erhalten wir den Algorithmus A_n+1. Auf dieselbe Weise erhalten wir den Algorithmus A_n+2 usw. So können wir eine beliebige Anzahl von Scheiben übertragen.

Mehr zur Problematik der Rekursion und Wiederholung sowie der Komplexität kann man in [SolAlg] nachlesen.

© APSIS GmbH , Polling, 2008