© APSIS GmbH ![]() , Polling,
2008
, Polling,
2008
zum Kapitel 10.
Übung 10.1: Entwickeln Sie ein Programm für neun Kreise mit einer Reihung. An Stelle einer Referenz auf den vorgewählten Kreis können sie einen int-Wert mit der Nummer eines der neun Kreise einlesen. Dieser Index der Reihung „zeigt“ auf den ausgewählten Kreis ähnlich wie eine Referenz. Sie können anschließend die gewünschte Aktion ("Bemalen" usw.) auswählen. Achten Sie jedoch darauf, dass die Kreise in derselben Reihenfolge angezeigt werden, wie die Methode zeichnen für sie aufgerufen wurde. Damit diese Ihrer Nummerierung entspricht, ist es zweckmäßig, vor dem Aufruf des Menüs alle neun Kreise zu zeichnen und anschließend zu verstecken; dann behalten sie ihre Positionen im Fenster während des gesamten Programmlaufs.
Übung 10.2: Schreiben Sie ein Hauptprogramm, das mit zwei Kommandozeilenparametern aufgerufen werden kann. Der Inhalt der beiden Parameter soll auf zwei Knöpfen (java.awt.Button oder javax.swing.JButton) erscheinen. Wenn das Programm mit weniger als zwei Kommandozeilenparametern aufgerufen wird, soll die Ausnahme aufgefangen werden. In diesem Fall sollen die Knöpfe mit einer Standardbeschriftung erscheinen.
Übung 10.3: Unter Permutationen verstehen wir alle (unterschiedlichen) Umordnungen einer Menge; z.B. alle Permutationen von 123 sind 123 132 213 231 312 321. Die Anzahl der Permutationen aus n Elementen ist n! (n! ist die mathematische Bezeichnung der Fakultät, des Produkts der ersten n natürlichen Zahlen). Dies ist mit Hilfe der mathematischen Induktion beweisbar (s. Kapitel 8.4.3.). Angenommen, wir haben alle Permutationen aus n-1 Elementen. Daraus erzeugen wir die Permutationen aus n Elementen, indem wir die Permutationen aus n-1 Elementen n-mal kopieren. Das n-te Element wird nun in der ersten Kopie vor das erste Element geschoben, in der zweiten vor das zweite usw.; in der n-1-sten Kopie vor das n-1-ste (also das letzte) Element, schließlich in der n-ten Kopie nach dem letzten Element. Wenn die Anzahl der Permutationen aus n-1 Elementen Pn-1 war, dann erhalten wir auf diese Weise n .Pn-1 verschiedene Permutationen. Für n=1 ist diese Anzahl 1. Wenn Pn-1 = (n-1)!, dann Pn = n .Pn-1 = n .(n-1)! = n!.
Entwickeln Sie nun eine Funktion für die rekursive Berechnung von Permutationen. In der rekursiven Funktion permutationen sollen Sie eine lokale Reihung anlegen, die die Permutationen aus n-1 Elementen enthält. Sie sollen diese in das Ergebnis (ebenfalls eine lokale zweidimensionale Reihung der Größe n! x n, ) n-mal kopieren und das letzte Element an die 1-ste, 2-te, … n-te Stelle einschieben. Eine geschickte Manipulation der Indizes ist hier der Schlüssel für eine elegante Lösung.
Fertigen Sie zwei Testtreiber für Ihre Klasse an: einen Stapeltesttreiber, der eine Reihung aus char-Elementen permutiert, sowie einen Dialogtesttreiber, der für eine eingegebene n die Ganzzahlen von 1 bis n permutiert.
Übung 10.4: Implementieren Sie die Schnittstelle IStapel mit Hilfe der Klasse java.util.Vector. Entscheiden Sie dabei zwischen Erwerben und Erben mit geeigneter Argumentation.
Übung 10.5: Überschreiben Sie die Methode eintragen der Klasse Stapel, indem Sie beim Indexüberlauf die Technik der dynamischen Reihungen verwenden.
Übung 10.6: Implementieren Sie die Schnittstelle IWarteschlange als Reihung (mit integriertem Testprogramm mit fest eingebauten Testfällen als main in der Klasse).
Im Stapel haben wir einen Index spitze geführt. In der Warteschlange müssen Sie zwei Indizes aeltestes und juengstes führen. Wenn ein Index das Ende der Reihung erreicht (überläuft), soll er bei 0 wieder angesetzt werden. Am einfachsten ist dies mit dem Restoperator % zu berechnen:
juengstes = (juengstes + 1) % inhalt.length; // zyklische Indizierung: beim Überlauf 0
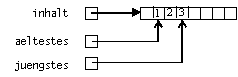
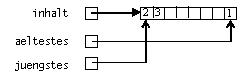
Abb: Warteschlange als Reihung und nach Überlauf
Diese Datenstruktur heißt auch Ringpuffer
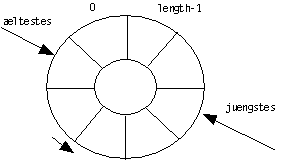
Abb.: Ringpuffer
Übung 10.7: Im Kapitel 9.2.8. haben wir erwähnt, dass die Multibehälter für primitive Werte ähnlich wie für Objekte programmiert werden können. Implementieren Sie also die Schnittstelle für eine Ganzzahl-Warteschlange ähnlich, wie in der Übung 10.6:
public interface IIntWarteschlange { public void entleeren(); public void eintragen(final int element) throws VollException; public int lesen() throws LeerException; … // usw. ähnlich wie lehrbuch.multi.IWarteschlange }
Programmieren Sie die zyklische Indizierung diesmal nicht mit dem Restoperator, sondern mit Verzweigungen.
Übung 10.8: In der Übung 4.4 haben wir die Klasse Tor kennen gelernt, mit der Tore an einem Werksgelände gesteuert werden können. Schreiben Sie nun eine Datenbehälterklasse Tore, die eine im Konstruktorparameter gegebene Anzahl von Tor-Objekten in einer Reihung verwaltet. Sie soll dieselben drei Methoden wie die Tor-Klasse veröffentlichen, jedoch mit je einem int-Parameter, der den Index des zu manipulierenden Tor-Objekts darstellt. Darüber hinaus soll sie noch eine Methode
public int anzahl();
veröffentlichen, die die Anzahl der verwalteten Tor-Objekte zurückgibt.
Schreiben Sie auch ein Hauptprogramm (main) mit zwei globalen Tore-Objekten und eine Prozedur. Diese hat zwei Parameter: ein Tore-Objekt und ein Index. Sie öffnet das entsprechende Tor und schließt es dann wieder. Rufen Sie die Prozedur so oft auf, dass alle Ihre Tor-Objekte geöffnet und geschlossen werden.
Wählen Sie das Profil der Prozedur so, dass Sie Ausnahmen, die aufgrund der Programmlogik nicht auftreten können, in der Prozedur behandeln (System.err.println für den Notfall, wenn sie doch auftreten würden), und nur die tatsächlich möglichen Ausnahmen weiterreichen.
Wo Sie die Ausnahmen behandeln (im Hauptprogramm oder in der Prozedur), entscheiden Sie danach, wo sie ausgelöst werden können oder aber auch nicht (am besten mit System.err.println).
Zeichnen Sie die Datenstruktur des Programms (alle Objekte und alle Referenzen, die auf sie zeigen).
Übung 10.11: Jetzt können Sie Ihre Schnittstelle ISackAlgebra aus der Übung 9.1 implementieren. Testen Sie Ihre Klasse.
Übung 10.9: Einen Vektor zu normalisieren bedeutet, alle ihre Elemente auf Werte zwischen –max und max zu setzen (wobei max Parameter der Normalisierung ist) so, dass das Verhältnis der Elemente zueinander bleibt. Dies kann in zwei Schritten durchgeführt werden: Zuerst muss das Element mit dem maximalen Wert gefunden werden, dann müssen alle Elemente mit max multipliziert und durch diesen (positiven) Wert dividiert werden.
Erweitern Sie nun die generische Klasse GVektor um die parametrisierte void-Methode normalisieren.Hierzu ist eine Erweiterung der Schnittstelle IElement nötig, die auch eine Vergleichsmethode und eine Methode zum Dividieren enthält.
Testen Sie Ihre Methode mit einer Elementklasse FloatElement, in deren Objekte float-Werte gespeichert werden können.
Übung 10.10: Reimplementieren Sie die GVektor-Klasse, indem Sie die Operationen (plus usw.) nicht als Mutatoren, sondern als Funktionen definieren.
Übung 10.11: Reimplementieren Sie die GMatrix-Klasse, indem Sie die Operationen nicht als Mutatoren, sondern als Funktionen definieren.
Übung 10.12: Programmieren Sie das Produkt zweier Matrizen nach der folgenden Regel: Das Element in der Zeile i und der Spalte j der Produktmatrix C ist das Skalarprodukt der i-ten Zeile der ersten Matrix A mit der j-ten Spalte der zweiten Matrix B. Hieraus ergibt sich folgende Formel für alle Elemente ci,j des Produkts zweier Matrizen mit den Elementen ai,j und bi,j :
![]()
d.h. jedes Element ci,j der Ergebnismatrix C (des Ergebnisses) mit den Indizes i und j ist die Summe der i-ten Zeile der ersten Matrix A und der j-ten Spalte der zweiten Matrix B. Aus dieser Formel ist ersichtlich, dass die Anzahl der Spalten in A gleich sein soll mit der Anzahl der Zeilen in B. (Die erste Dimension von A muss mit der zweiten Dimension von B gleich sein.) Die Ergebnismatrix C hat so viele Zeilen wie A und so viele Spalten wie B: Wenn A ein n x l und B eine l x m Matrix ist, dann wird das Produkt C eine n x m Matrix werden.
Für die Programmierung des Matrixprodukts ist eine dreifach geschachtelte Wiederholung nötig.
Schreiben Sie auch ein Testprogramm für Ihre Matrixklasse, in welchem Sie sie mit einer Ganzzahl- und für eine Bruchklasse ausprägen. Im Stapeltesttreiber sollen Sie die Matrizen (der Größe 2x3 und 3x4) als Konstanten definieren, ihre Summen und Produkte errechnen und am Bildschirm in Matrixform ausgeben.
Übung 10.13: Programmieren Sie einen Assoziativspeicher als Assoziativtabelle. Die Schnittstelle eines (allgemeinen) Assoziativspeichers ist folgende:
public interface IAssoTab { public void entleeren(); public void eintragen(final Object schluessel, final Object element) throws VollException; // const // ensures !istLeer() public Object finden(final Object schluessel) throws NichtVorhandenException; // const // requires vorhanden(schluessel) public boolean vorhanden(final Object schluessel); // const public boolean istLeer(); // const public boolean istVoll(); // const public class NichtVorhandenException extends Exception {}
Definieren Sie nun die Datenstruktur der Klasse AssoTab und programmieren Sie ihre Methoden. Prägen Sie Ihren Assoziativspeicher für ein Telefonbuch aus, in dem Sie den Nachnamen als Schlüssel, Vornamen und Telefonnummer als Element speichern. Die Größe der Tabelle sollte als Konstruktorparameter angegeben werden. Schreiben Sie dazu ein einfaches Dialogtestprogramm. Vergessen Sie dabei die Persistenzoperationen nicht: Über einen Menüpunkt sollte Ihre Tabelle in eine Datei, deren Name eingegeben wird, gespeichert bzw. von dort gelesen werden können. Hierzu muss die Elementklasse die Schnittstelle java.io.Serializable implementieren.
Übung 10.14: Testen Sie die obige Klasse mit Ihrem Programm aus der Übung 9.10. Wegen der unveränderten Profile dürften Sie keine Veränderung des Programmverhaltens wahrnehmen.
Übung 10.15: Implementieren Sie die Kopieroperation und den Vergleich des Stapels mit der Reihungsimplementierung mit der Technik der rekursiven Abarbeitung.
Übung 10.16: Erstellen Sie einen Ganzzahlstapel (mit Elementtyp int) als Reihung und erweitern Sie ihn so, dass er auch eine Funktion exportiert, die die Summe aller gestapelten Zahlen liefert. Implementieren Sie diese Methode rekursiv.
Übung 10.17: Implementieren Sie die Kopieroperation und den Vergleich der Listenimplementierung der Warteschlange mit der Technik der rekursiven Abarbeitung.
Übung 10.18: Eine Warteschlange kann auch mit einem Anker als ein vorwärts verketteter Ring implementiert werden. Der Anker referenziert den jüngsten Knoten; dessen Verkettung referenziert den ältesten Knoten. Implementieren Sie nun die Warteschlange auf diese Weise.
© APSIS GmbH ![]() , Polling,
2008
, Polling,
2008