| |
T H E O R Y O F P O L A R - P L A N I M E T E R S
to show how it works, that
a PolarPlanimeter measures an area by tracing its boundary
--------------------------------------------------------------
The basic idea and the drawing is taken from:
"KLEINE ENZYKLOPAEDIE MATHEMATIK" Harry Deutsch,
Frankfurt a.M. (1972)
Chapter "Integralrechnung", Pages 467 + 468
--------------------------------------------------------------
The POLAR PLANIMETER was invented around 1850 by J.Amsler and
was used until the 1980s by engineers, physicists and others
for the rapid and accurate determination of plane surface
areas, when no mathematical function of their boundaries was
available. Examples: Determination of reservoir capacities
from scaled aerial photographs, or "Integration" by measuring
an area under the curve, drawn from experiment datas. A Polar-
Planimeter consists of 3 parts: The PolArm P, the TracerArm T
and a Carriage with the measurement device M. M consists of a
vertical measuring wheel with graduated scale, vernier and a
dial, which counts the number of full turns of M.
The PoleArm and the TracerArm are pivoted together at point A
and are free to rotate about a weighted needle point (or pole)
O. The TracerArm has the measuring device M on one end and the
TracerPoint S on the other end. With this TracerPoint the
boundaries of an area F has to be carefully followed until it
has returned to the starting point S. The measuring device M
will show a decimal number related to the area space F.
The diagram shows the dynamic relations:
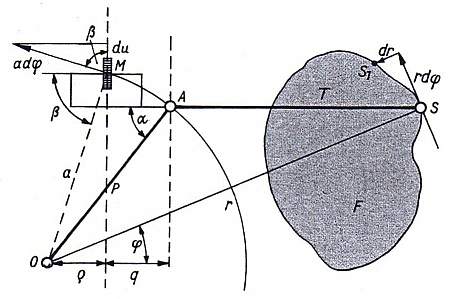 Cosine Rule:
r2 = P2 + T2 - 2PT * cos(180° - α)
------v------
- cos α
---v---
+ 2T * P * cos α
----v----
r2 = P2 + T2 + 2T * ( ρ + q ) [1]
When the plane of the wheel M goes through the pole O
( β = 90° ), than ρ = 0 and equation [1] becomes:
g2 = P2 + T2 + 2Tq [2]
where g is called "Radius of the Base Circle". Therefore
G is the "Area of the Base Circle" and is a constant of
the PolarPlanimeter:
G = π * g2 [3]
The subtraction [1] - [2] becomes:
r2 - g2 = 2Tρ -->> ρ = ( ½ r2 - ½ g2 ) / T [4]
The movement of the TracerPoint S to a neighbor point S1
could be separated in a tangential component rdφ and a
radial component dr.
For the way around the closed boundary of the area the
sum of all dr equals zero - therefore the influence of
dr on the motion of the wheel M is cancelled out.
With a circular move from S to S1 with angle φ > 0 and
r constant, the triangle OSA doesn't change and M moves
rectangular to distance OM = a with adφ . M turns
therefore with the distance du rectangular to its axis:
du = a * dφ * cos β = a * cos β * dφ = ρ * dφ
----v----
ρ
Substitution ρ with [4] becomes:
du = ( ½ r2 dφ - ½ g2 dφ ) / T [5]
The general form of an area F in polar coordinates:
2π
F = ½ * ∫ r2 dφ [6]
Equation [5] transformed:
½ r2 dφ = T * du + ½ g2 dφ
and substituted in [6] to solve the integral:
F = ∫ ( T * du + ½ g2 dφ )
---v--- ---v---
F = T * U + ½ g2 * ( φ2 - φ1 ) [7]
It is g2 = const. After a full trace we get φ2 = φ1 , if
the pole O is outside the area F , and φ2 = 2π + φ1 , if
the pole is inside the area F . In the first case the
second term of [7] is zero, in the second case this term
equals ½ g2 * 2π = G ( see equ.[3] ).
The sum of all du is U. The measuring wheel M, with its
diameter D has made x turns along the distance U:
U = π D x [8]
If the pole is outside the area F , we get with [7],[8]:
F = T * π D * x = k * x [9]
---v---
k
The constant k is specific to the used PolarPlanimeter,
and is for example:
k1 = 100 square cm
or k2 = 15 square inch
If the pole is inside the area F, the result is
F = G + k * n
where G, the "Area of the Base Circle" (see equ.[3],[7]) is a
constant for the used PolarPlanimeter and has to be given or
experimentally calculated.
The mechanic of the PolarPlanimeter may require that the
boundary of an area has to be traced clockwise in order to
count a positive result in the measuring device M.
"Many Thanks!"
--------------
Prof. Dr. Dietmar Goebel & Prof. Dr. Angela Schwenk from the
Mathematics Department of our TFH made valuable suggestions &
corrections to my 1st draft of this site - Dr. Michael Giehl
from the FU-Berlin / Klinikum »Benjamin Franklin« took effords
to proof that this site in HTML is much smaller as a PDF-File.
==============================================================
Look at W.Bluemich's
Cosine Rule:
r2 = P2 + T2 - 2PT * cos(180° - α)
------v------
- cos α
---v---
+ 2T * P * cos α
----v----
r2 = P2 + T2 + 2T * ( ρ + q ) [1]
When the plane of the wheel M goes through the pole O
( β = 90° ), than ρ = 0 and equation [1] becomes:
g2 = P2 + T2 + 2Tq [2]
where g is called "Radius of the Base Circle". Therefore
G is the "Area of the Base Circle" and is a constant of
the PolarPlanimeter:
G = π * g2 [3]
The subtraction [1] - [2] becomes:
r2 - g2 = 2Tρ -->> ρ = ( ½ r2 - ½ g2 ) / T [4]
The movement of the TracerPoint S to a neighbor point S1
could be separated in a tangential component rdφ and a
radial component dr.
For the way around the closed boundary of the area the
sum of all dr equals zero - therefore the influence of
dr on the motion of the wheel M is cancelled out.
With a circular move from S to S1 with angle φ > 0 and
r constant, the triangle OSA doesn't change and M moves
rectangular to distance OM = a with adφ . M turns
therefore with the distance du rectangular to its axis:
du = a * dφ * cos β = a * cos β * dφ = ρ * dφ
----v----
ρ
Substitution ρ with [4] becomes:
du = ( ½ r2 dφ - ½ g2 dφ ) / T [5]
The general form of an area F in polar coordinates:
2π
F = ½ * ∫ r2 dφ [6]
Equation [5] transformed:
½ r2 dφ = T * du + ½ g2 dφ
and substituted in [6] to solve the integral:
F = ∫ ( T * du + ½ g2 dφ )
---v--- ---v---
F = T * U + ½ g2 * ( φ2 - φ1 ) [7]
It is g2 = const. After a full trace we get φ2 = φ1 , if
the pole O is outside the area F , and φ2 = 2π + φ1 , if
the pole is inside the area F . In the first case the
second term of [7] is zero, in the second case this term
equals ½ g2 * 2π = G ( see equ.[3] ).
The sum of all du is U. The measuring wheel M, with its
diameter D has made x turns along the distance U:
U = π D x [8]
If the pole is outside the area F , we get with [7],[8]:
F = T * π D * x = k * x [9]
---v---
k
The constant k is specific to the used PolarPlanimeter,
and is for example:
k1 = 100 square cm
or k2 = 15 square inch
If the pole is inside the area F, the result is
F = G + k * n
where G, the "Area of the Base Circle" (see equ.[3],[7]) is a
constant for the used PolarPlanimeter and has to be given or
experimentally calculated.
The mechanic of the PolarPlanimeter may require that the
boundary of an area has to be traced clockwise in order to
count a positive result in the measuring device M.
"Many Thanks!"
--------------
Prof. Dr. Dietmar Goebel & Prof. Dr. Angela Schwenk from the
Mathematics Department of our TFH made valuable suggestions &
corrections to my 1st draft of this site - Dr. Michael Giehl
from the FU-Berlin / Klinikum »Benjamin Franklin« took effords
to proof that this site in HTML is much smaller as a PDF-File.
==============================================================
Look at W.Bluemich's  alternative Approach...
==============================================================
TO THE PLANIMETER COLLECTION ...
impressum:
**************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 11/11/07 alternative Approach...
==============================================================
TO THE PLANIMETER COLLECTION ...
impressum:
**************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 11/11/07
|
 Cosine Rule:
r2 = P2 + T2 - 2PT * cos(180° - α)
------v------
- cos α
---v---
+ 2T * P * cos α
----v----
r2 = P2 + T2 + 2T * ( ρ + q ) [1]
When the plane of the wheel M goes through the pole O
( β = 90° ), than ρ = 0 and equation [1] becomes:
g2 = P2 + T2 + 2Tq [2]
where g is called "Radius of the Base Circle". Therefore
G is the "Area of the Base Circle" and is a constant of
the PolarPlanimeter:
G = π * g2 [3]
The subtraction [1] - [2] becomes:
r2 - g2 = 2Tρ -->> ρ = ( ½ r2 - ½ g2 ) / T [4]
The movement of the TracerPoint S to a neighbor point S1
could be separated in a tangential component rdφ and a
radial component dr.
For the way around the closed boundary of the area the
sum of all dr equals zero - therefore the influence of
dr on the motion of the wheel M is cancelled out.
With a circular move from S to S1 with angle φ > 0 and
r constant, the triangle OSA doesn't change and M moves
rectangular to distance OM = a with adφ . M turns
therefore with the distance du rectangular to its axis:
du = a * dφ * cos β = a * cos β * dφ = ρ * dφ
----v----
ρ
Substitution ρ with [4] becomes:
du = ( ½ r2 dφ - ½ g2 dφ ) / T [5]
The general form of an area F in polar coordinates:
2π
F = ½ * ∫ r2 dφ [6]
Equation [5] transformed:
½ r2 dφ = T * du + ½ g2 dφ
and substituted in [6] to solve the integral:
F = ∫ ( T * du + ½ g2 dφ )
---v--- ---v---
F = T * U + ½ g2 * ( φ2 - φ1 ) [7]
It is g2 = const. After a full trace we get φ2 = φ1 , if
the pole O is outside the area F , and φ2 = 2π + φ1 , if
the pole is inside the area F . In the first case the
second term of [7] is zero, in the second case this term
equals ½ g2 * 2π = G ( see equ.[3] ).
The sum of all du is U. The measuring wheel M, with its
diameter D has made x turns along the distance U:
U = π D x [8]
If the pole is outside the area F , we get with [7],[8]:
F = T * π D * x = k * x [9]
---v---
k
The constant k is specific to the used PolarPlanimeter,
and is for example:
k1 = 100 square cm
or k2 = 15 square inch
If the pole is inside the area F, the result is
F = G + k * n
where G, the "Area of the Base Circle" (see equ.[3],[7]) is a
constant for the used PolarPlanimeter and has to be given or
experimentally calculated.
The mechanic of the PolarPlanimeter may require that the
boundary of an area has to be traced clockwise in order to
count a positive result in the measuring device M.
"Many Thanks!"
--------------
Prof. Dr. Dietmar Goebel & Prof. Dr. Angela Schwenk from the
Mathematics Department of our TFH made valuable suggestions &
corrections to my 1st draft of this site - Dr. Michael Giehl
from the FU-Berlin / Klinikum »Benjamin Franklin« took effords
to proof that this site in HTML is much smaller as a PDF-File.
==============================================================
Look at W.Bluemich's
Cosine Rule:
r2 = P2 + T2 - 2PT * cos(180° - α)
------v------
- cos α
---v---
+ 2T * P * cos α
----v----
r2 = P2 + T2 + 2T * ( ρ + q ) [1]
When the plane of the wheel M goes through the pole O
( β = 90° ), than ρ = 0 and equation [1] becomes:
g2 = P2 + T2 + 2Tq [2]
where g is called "Radius of the Base Circle". Therefore
G is the "Area of the Base Circle" and is a constant of
the PolarPlanimeter:
G = π * g2 [3]
The subtraction [1] - [2] becomes:
r2 - g2 = 2Tρ -->> ρ = ( ½ r2 - ½ g2 ) / T [4]
The movement of the TracerPoint S to a neighbor point S1
could be separated in a tangential component rdφ and a
radial component dr.
For the way around the closed boundary of the area the
sum of all dr equals zero - therefore the influence of
dr on the motion of the wheel M is cancelled out.
With a circular move from S to S1 with angle φ > 0 and
r constant, the triangle OSA doesn't change and M moves
rectangular to distance OM = a with adφ . M turns
therefore with the distance du rectangular to its axis:
du = a * dφ * cos β = a * cos β * dφ = ρ * dφ
----v----
ρ
Substitution ρ with [4] becomes:
du = ( ½ r2 dφ - ½ g2 dφ ) / T [5]
The general form of an area F in polar coordinates:
2π
F = ½ * ∫ r2 dφ [6]
Equation [5] transformed:
½ r2 dφ = T * du + ½ g2 dφ
and substituted in [6] to solve the integral:
F = ∫ ( T * du + ½ g2 dφ )
---v--- ---v---
F = T * U + ½ g2 * ( φ2 - φ1 ) [7]
It is g2 = const. After a full trace we get φ2 = φ1 , if
the pole O is outside the area F , and φ2 = 2π + φ1 , if
the pole is inside the area F . In the first case the
second term of [7] is zero, in the second case this term
equals ½ g2 * 2π = G ( see equ.[3] ).
The sum of all du is U. The measuring wheel M, with its
diameter D has made x turns along the distance U:
U = π D x [8]
If the pole is outside the area F , we get with [7],[8]:
F = T * π D * x = k * x [9]
---v---
k
The constant k is specific to the used PolarPlanimeter,
and is for example:
k1 = 100 square cm
or k2 = 15 square inch
If the pole is inside the area F, the result is
F = G + k * n
where G, the "Area of the Base Circle" (see equ.[3],[7]) is a
constant for the used PolarPlanimeter and has to be given or
experimentally calculated.
The mechanic of the PolarPlanimeter may require that the
boundary of an area has to be traced clockwise in order to
count a positive result in the measuring device M.
"Many Thanks!"
--------------
Prof. Dr. Dietmar Goebel & Prof. Dr. Angela Schwenk from the
Mathematics Department of our TFH made valuable suggestions &
corrections to my 1st draft of this site - Dr. Michael Giehl
from the FU-Berlin / Klinikum »Benjamin Franklin« took effords
to proof that this site in HTML is much smaller as a PDF-File.
==============================================================
Look at W.Bluemich's 