THE H A F F PROPORTIONAL DIVIDER (= Reduktions-Zirkel in German) Model 195aE
********************************************************************************
PURPOSE: Engineers have used this tool to transfer proportions from one drawing
to a new drawing in bigger or smaller scale. Open-air painters used it to trans-
fer distances in the landscape or art painters took proportions of the beautiful
model to sketch it on paper - as base of the artwork in mind.
USAGE: With closed legs loosen the TOP SCREW. With the OPPOSITE SCREW move
the axle up or down to the SCALE-MARK of your choice. Tighten the TOP-SCREW.
Open the LEGS, sample the original distance with ONE SIDE - the OPPOSITE SIDE
will be in the desired SCALE-PROPORTION.
There are 2 SCALE-MARKS:
o In »LINES« the sampled DISTANCES are set in proportion.
( 1:1 ; 4:3 ; 3:2 ; 5:3 ; 2 ; 2.5 ; 3 ; 4 ; 5 ; ... 9 ; 10 )
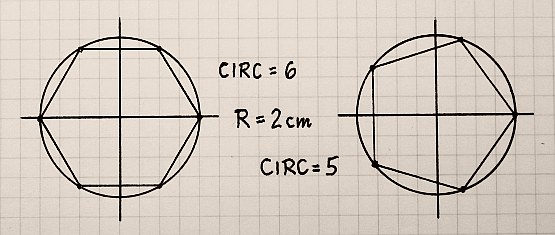
o In »CIRCLES« when its D I A M E T E R IS TAKEN AS THE SAMPLE,
the OPPOSITE SIDE will cut the circumference in equal sections:
( 4 ; GS ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; ... 16 ; ... 20 )
E.g.:
»4« will make 4 Segments ( = 90° Sectors = Corners of a Square ),
»5« will make 5 Segments ( = 72° Sectors = Corners of a Pentagon),
...
out of the full circle ...
 The M A R K »GS« = "Goldener Schnitt" = "Golden Cut" = "THE GOLDEN RATIO"
--------------------------------------------------------------------------------
Separates a LINE AB in C to the well known proportion:
|===============================|==================|
A C B
AB/AC = AC/CB = 2/( SQRT(5) - 1 ) = 1.618033988749... = PHI = Φ (*)
It is attributed as "divine", "beautiful", "harmonious", "aesthetics", ...
in ART & ARCHITECTURE and has some UNIQUE PROPERTIES in MATHEMATICS too ...
Φ2 = Φ + 1 1/Φ = Φ - 1 Φ = 1 + 1/Φ Φ = 1+1/(1+1/(1+1/(1+1/(1+1/ ...))...)
How this (*) FORMULA came out of ???
********************************************************************************
[1st] A GEOMETRICAL CONSTRUCTION ...
The M A R K »GS« = "Goldener Schnitt" = "Golden Cut" = "THE GOLDEN RATIO"
--------------------------------------------------------------------------------
Separates a LINE AB in C to the well known proportion:
|===============================|==================|
A C B
AB/AC = AC/CB = 2/( SQRT(5) - 1 ) = 1.618033988749... = PHI = Φ (*)
It is attributed as "divine", "beautiful", "harmonious", "aesthetics", ...
in ART & ARCHITECTURE and has some UNIQUE PROPERTIES in MATHEMATICS too ...
Φ2 = Φ + 1 1/Φ = Φ - 1 Φ = 1 + 1/Φ Φ = 1+1/(1+1/(1+1/(1+1/(1+1/ ...))...)
How this (*) FORMULA came out of ???
********************************************************************************
[1st] A GEOMETRICAL CONSTRUCTION ...
 IF you want to find the »GS«-POINT (C) in a given LINE-AB =!= 2, THAN ...
o Draw a rectangular 1/2 LENGTH-OF-LINE-AB =!= 1 in POINT-B to POINT-X
o Draw the HYPOTENUSE of this RECTANGLE from POINT-A to POINT-X
o With PYTHAGORAS's RULE the lenth of the HYPOTENUSE is SQRT(5)
o Put the COMPASS in X: (a) Mark the LENGHT = 1 on the HYPOTENUSE
o Put the COMPASS in A: (b) Transfer THIS POINT to LINE-AB as POINT-C
o POINT-C is »GS«, the "Golden Cut" of LINE-AB
The GEOMETRICAL CONSTRUCTION showed the relation ...
AC SQRT(5) - 1 SQRT(5) - 1
---- = --------------------- = ------------- = 1.618 = Φ
CB 2 - ( SQRT(5) - 1 ) 3 - SQRT(5) =====
AB 2
---- = --------------------- = 1.618 = Φ
AC SQRT(5) - 1 =====
********************************************************************************
[2nd] AN ANALYTICAL SOLUTION ...
From (*) AB / AC = AC / CB
we get AC2 = AB * CB and let AB =!= 2 = AC + CB
than CB = 2 - AC
now substituted
AC2 = 2 * ( 2 - AC ) follows AC2 + 2*AC - 4 = 0
Using the well known formula to solve a squared equations ...
x2 + px + q = 0 ===>> x1,2 = - p/2 +/- SQRT( (p/2)2 - q )
AC = - 1 +/- SQRT( 1 + 4 )
= SQRT(5) - 1 { only + is real }
... we get AB / AC = 2 / ( SQRT(5) - 1 ) = 1.618 = Φ qed.
********************************************************************************
A wonderful BOOK about "Proportional Harmonies in Nature, Art & Architecture"...
IF you want to find the »GS«-POINT (C) in a given LINE-AB =!= 2, THAN ...
o Draw a rectangular 1/2 LENGTH-OF-LINE-AB =!= 1 in POINT-B to POINT-X
o Draw the HYPOTENUSE of this RECTANGLE from POINT-A to POINT-X
o With PYTHAGORAS's RULE the lenth of the HYPOTENUSE is SQRT(5)
o Put the COMPASS in X: (a) Mark the LENGHT = 1 on the HYPOTENUSE
o Put the COMPASS in A: (b) Transfer THIS POINT to LINE-AB as POINT-C
o POINT-C is »GS«, the "Golden Cut" of LINE-AB
The GEOMETRICAL CONSTRUCTION showed the relation ...
AC SQRT(5) - 1 SQRT(5) - 1
---- = --------------------- = ------------- = 1.618 = Φ
CB 2 - ( SQRT(5) - 1 ) 3 - SQRT(5) =====
AB 2
---- = --------------------- = 1.618 = Φ
AC SQRT(5) - 1 =====
********************************************************************************
[2nd] AN ANALYTICAL SOLUTION ...
From (*) AB / AC = AC / CB
we get AC2 = AB * CB and let AB =!= 2 = AC + CB
than CB = 2 - AC
now substituted
AC2 = 2 * ( 2 - AC ) follows AC2 + 2*AC - 4 = 0
Using the well known formula to solve a squared equations ...
x2 + px + q = 0 ===>> x1,2 = - p/2 +/- SQRT( (p/2)2 - q )
AC = - 1 +/- SQRT( 1 + 4 )
= SQRT(5) - 1 { only + is real }
... we get AB / AC = 2 / ( SQRT(5) - 1 ) = 1.618 = Φ qed.
********************************************************************************
A wonderful BOOK about "Proportional Harmonies in Nature, Art & Architecture"...
 ISBN 978-1-59030-259-0
György Doczi » THE POWER OF LIMITS « (2005) Shambhala, Boston & London
eg. FIBONACCI-Serie: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
(a) Each number is the sum of the two previous ones
(b) Any number in this serie divided by the following one is ~0.618...
and any number divided by the previous one is ~1.618... = Φ
********************************************************************************
REMARK: As a "Rule-Of-Thumb" 60% / 40% is a good guess of the »GS«-POINT (C)
PART TWO = AN ENGINEERING APPROACH = BOWEN Model 770 ...
Back to the ENGINEERING TOOLS Main Page
impressum:
********************************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 02/02/23 ISBN 978-1-59030-259-0
György Doczi » THE POWER OF LIMITS « (2005) Shambhala, Boston & London
eg. FIBONACCI-Serie: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
(a) Each number is the sum of the two previous ones
(b) Any number in this serie divided by the following one is ~0.618...
and any number divided by the previous one is ~1.618... = Φ
********************************************************************************
REMARK: As a "Rule-Of-Thumb" 60% / 40% is a good guess of the »GS«-POINT (C)
PART TWO = AN ENGINEERING APPROACH = BOWEN Model 770 ...
Back to the ENGINEERING TOOLS Main Page
impressum:
********************************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 02/02/23
|

 The M A R K »GS« = "Goldener Schnitt" = "Golden Cut" = "THE GOLDEN RATIO"
--------------------------------------------------------------------------------
Separates a LINE AB in C to the well known proportion:
|===============================|==================|
A C B
AB/AC = AC/CB = 2/( SQRT(5) - 1 ) = 1.618033988749... = PHI = Φ (*)
It is attributed as "divine", "beautiful", "harmonious", "aesthetics", ...
in ART & ARCHITECTURE and has some UNIQUE PROPERTIES in MATHEMATICS too ...
Φ2 = Φ + 1 1/Φ = Φ - 1 Φ = 1 + 1/Φ Φ = 1+1/(1+1/(1+1/(1+1/(1+1/ ...))...)
How this (*) FORMULA came out of ???
********************************************************************************
[1st] A GEOMETRICAL CONSTRUCTION ...
The M A R K »GS« = "Goldener Schnitt" = "Golden Cut" = "THE GOLDEN RATIO"
--------------------------------------------------------------------------------
Separates a LINE AB in C to the well known proportion:
|===============================|==================|
A C B
AB/AC = AC/CB = 2/( SQRT(5) - 1 ) = 1.618033988749... = PHI = Φ (*)
It is attributed as "divine", "beautiful", "harmonious", "aesthetics", ...
in ART & ARCHITECTURE and has some UNIQUE PROPERTIES in MATHEMATICS too ...
Φ2 = Φ + 1 1/Φ = Φ - 1 Φ = 1 + 1/Φ Φ = 1+1/(1+1/(1+1/(1+1/(1+1/ ...))...)
How this (*) FORMULA came out of ???
********************************************************************************
[1st] A GEOMETRICAL CONSTRUCTION ...
 IF you want to find the »GS«-POINT (C) in a given LINE-AB =!= 2, THAN ...
o Draw a rectangular 1/2 LENGTH-OF-LINE-AB =!= 1 in POINT-B to POINT-X
o Draw the HYPOTENUSE of this RECTANGLE from POINT-A to POINT-X
o With PYTHAGORAS's RULE the lenth of the HYPOTENUSE is SQRT(5)
o Put the COMPASS in X: (a) Mark the LENGHT = 1 on the HYPOTENUSE
o Put the COMPASS in A: (b) Transfer THIS POINT to LINE-AB as POINT-C
o POINT-C is »GS«, the "Golden Cut" of LINE-AB
The GEOMETRICAL CONSTRUCTION showed the relation ...
AC SQRT(5) - 1 SQRT(5) - 1
---- = --------------------- = ------------- = 1.618 = Φ
CB 2 - ( SQRT(5) - 1 ) 3 - SQRT(5) =====
AB 2
---- = --------------------- = 1.618 = Φ
AC SQRT(5) - 1 =====
********************************************************************************
[2nd] AN ANALYTICAL SOLUTION ...
From (*) AB / AC = AC / CB
we get AC2 = AB * CB and let AB =!= 2 = AC + CB
than CB = 2 - AC
now substituted
AC2 = 2 * ( 2 - AC ) follows AC2 + 2*AC - 4 = 0
Using the well known formula to solve a squared equations ...
x2 + px + q = 0 ===>> x1,2 = - p/2 +/- SQRT( (p/2)2 - q )
AC = - 1 +/- SQRT( 1 + 4 )
= SQRT(5) - 1 { only + is real }
... we get AB / AC = 2 / ( SQRT(5) - 1 ) = 1.618 = Φ qed.
********************************************************************************
A wonderful BOOK about "Proportional Harmonies in Nature, Art & Architecture"...
IF you want to find the »GS«-POINT (C) in a given LINE-AB =!= 2, THAN ...
o Draw a rectangular 1/2 LENGTH-OF-LINE-AB =!= 1 in POINT-B to POINT-X
o Draw the HYPOTENUSE of this RECTANGLE from POINT-A to POINT-X
o With PYTHAGORAS's RULE the lenth of the HYPOTENUSE is SQRT(5)
o Put the COMPASS in X: (a) Mark the LENGHT = 1 on the HYPOTENUSE
o Put the COMPASS in A: (b) Transfer THIS POINT to LINE-AB as POINT-C
o POINT-C is »GS«, the "Golden Cut" of LINE-AB
The GEOMETRICAL CONSTRUCTION showed the relation ...
AC SQRT(5) - 1 SQRT(5) - 1
---- = --------------------- = ------------- = 1.618 = Φ
CB 2 - ( SQRT(5) - 1 ) 3 - SQRT(5) =====
AB 2
---- = --------------------- = 1.618 = Φ
AC SQRT(5) - 1 =====
********************************************************************************
[2nd] AN ANALYTICAL SOLUTION ...
From (*) AB / AC = AC / CB
we get AC2 = AB * CB and let AB =!= 2 = AC + CB
than CB = 2 - AC
now substituted
AC2 = 2 * ( 2 - AC ) follows AC2 + 2*AC - 4 = 0
Using the well known formula to solve a squared equations ...
x2 + px + q = 0 ===>> x1,2 = - p/2 +/- SQRT( (p/2)2 - q )
AC = - 1 +/- SQRT( 1 + 4 )
= SQRT(5) - 1 { only + is real }
... we get AB / AC = 2 / ( SQRT(5) - 1 ) = 1.618 = Φ qed.
********************************************************************************
A wonderful BOOK about "Proportional Harmonies in Nature, Art & Architecture"...
 ISBN 978-1-59030-259-0
György Doczi » THE POWER OF LIMITS « (2005) Shambhala, Boston & London
eg. FIBONACCI-Serie: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
(a) Each number is the sum of the two previous ones
(b) Any number in this serie divided by the following one is ~0.618...
and any number divided by the previous one is ~1.618... = Φ
********************************************************************************
REMARK: As a "Rule-Of-Thumb" 60% / 40% is a good guess of the »GS«-POINT (C)
ISBN 978-1-59030-259-0
György Doczi » THE POWER OF LIMITS « (2005) Shambhala, Boston & London
eg. FIBONACCI-Serie: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
(a) Each number is the sum of the two previous ones
(b) Any number in this serie divided by the following one is ~0.618...
and any number divided by the previous one is ~1.618... = Φ
********************************************************************************
REMARK: As a "Rule-Of-Thumb" 60% / 40% is a good guess of the »GS«-POINT (C)