|
|
|
Kurzbeschreibung
der Diplomarbeit von A. J. Kleier
mit dem
Titel:
|
|
NUMERISCHE SIMULATION VON
FESTSTOFFSTRÖMUNGEN IN EINEM REDUKTIONSSCHACHT
|
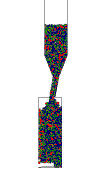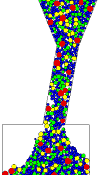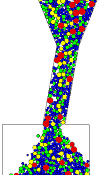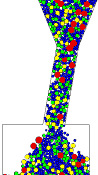 |
|
Simulation der
Schüttgutbewegung im Spinnenbein (Zufuhr zum Reduktionsschacht)
|
|
|
Eines der komplexesten Aufgabengebiete der
mechanischen Verfahrenstechnik ist die Beschreibung und
Erforschung des Fließ- und Lagerungsverhaltens von
Schüttgütern. In dieser Arbeit soll das Fließverhalten
von
Erz in einem Schacht untersucht werden. Diese Untersuchung wird mittels
einer Computersimulation durchgeführt.
Mit dem Programm PFC2D (Particle Flow Code)
von Itasca Consultants,
welches mit diskreten Körpern
arbeitet, ist es möglich, individuell die Bewegung jedes einzelnen
Körpers zu verfolgen. Damit bietet dieses Verfahren der
numerischen Modellierung nahezu einzigartige Möglichkeiten der
Untersuchung des Fließ- und Lagerverhaltens von
Schüttungen.
Untersucht wird das Fließverhalten von
Stückerz in einem Reduktionsschacht, der Teil des
COREX®-Prozesses
zur Roheisenherstellung ist. Zunächst wird der
Schacht durch ein 2D-Ersatzmodell abgebildet. Ziel der Untersuchung ist
die Prüfung des Ist-Zustandes mit einem
Referenzmodell und die Durchführung von Parameterstudien, um das
Verhalten bei veränderten
Randbedingungen zu prüfen.
|
|
Gegenstand der Untersuchung ist, wie oben
erwähnt, die Simulation des Fließverhaltens eines granularen
Feststoffes in einem
Reduktionsschacht. Dieses siloartige Bauteil ist eines der
Hauptbestandteile des
COREX®-Prozesses,
einem speziellen Schmelzreduktionsverfahren
zur Herstellung von Roheisen aus Kohle und Eisenerz.
Im Vergleich zum konventionellen Hochofenverfahren kann beim COREX®-
Prozeß nicht verkokbare Kohle direkt als Energieträger und
Reduktionsmittel eingesetzt und Eisenerz in Form von
Stückerz verwendet werden. COREX® ersetzt somit die Kokerei,
Sinteranlage und den Hochofen.
In der folgenden Abbildung ist ein
Fließbild des Verfahrens dargestellt:
|

|
|
Der Particle Flow Code in 2 Dimensionen
wurde zur Modellierung verwendet. PFC
basiert auf der Distinct
Element Method und modelliert die Wechselwirkung von kreis- (2D) bzw.
kugelförmigen (3D) Partikeln.
Zusätzlich stehen Wandelemente zur Verfügung, die i.A. als
Ränder des numerischen Modells und zum Aufbringen der
Randbedingungen verwendet werden. Wände wechselwirken nur mit den
Partikeln, d.h. eine Wand-Wand-Wechselwirkung findet nicht
statt. Die Partikel sind starr, d.h. nicht-deformierbar.
Der explizite Berechnungsalgorithmus besteht
aus
zwei Teilen. Die Newton'schen Bewegungsgleichungen
werden in jedem Rechenschritt für jeden Partikel gelöst,
woraus sich neue Positionen der Partikel ergeben. Mit Hilfe eines
Kraft-Verschiebungs-Gesetzes werden dann im zweiten Teil die sich
daraus ergebenden neuen Kontaktkräfte berechnet. Kontakte
werden vom Programm zu jedem Zeitpunkt vollautomatisch erkannt. Es gibt
zwei Kontaktarten; Punktkontakte, die nur der
Kraftübertragung dienen, und Parallelkontakte, die eine Art
Zementierung darstellen und sowohl Kräfte als auch Momente
übertragen können.
Für die hier vorgestellten Berechnungen
wird nur das Punktkontakt-Modell mit einem linearen
Kraft-Verschiebungs-Gesetz benutzt. Dabei werden den Kontakten Normal-
und Schersteifigkeiten zugewiesen,
die es erlauben, Normal- und Scherbewegungen getrennt zu behandeln. Ein
Reibungsmodell wird verwendet,
um die maximal zulässige Scherkraft an einem Kontakt über
einen Reibungskoeffizienten aus der wirkenden
Normalkraft zu berechnen. Das makroskopische Verhalten des Modells wird
durch die mikroskopischen Parameter der
Partikel (Steifigkeiten, Reibungswinkel, Festigkeiten) bestimmt.
PFC besitzt zusätzlich eine interne Programmiersprache (FISH), die den Zugriff auf alle physikalischen und Modellparameter erlaubt, und von der einfachen Funktionsberechnung bis hin zur kompletten Steuerung einer Modellierung eingesetzt werden kann. Da PFC einen expliziten
Zeitintegrationsalgorithmus verwendet, kann das Modell zu jedem
Zeitpunkt
der Modellierung modifiziert werden. Gleichzeitig erfordert der
explizite Algorithmus einen Zeitschritt, der zur
Integration der Bewegungsgleichungen benötigt wird und so
gewählt wird, daß sich die physikalischen Informationen in
einem
Rechenschritt maximal von einem Partikel bis zum nächsten Partikel
ausbreiten können. Die Größe des
Zeitschritts wird von der Masse und den Kontaktsteifigkeiten der
einzelnen Partikel bestimmt.
Da nur ein Zeitschritt für das gesamte Modell verwendet wird, wird
der minimale Wert des Gesamtmodells verwendet.
Eine 3D-Modellierung mit Partikeln realistischer Größe führt zu einem aus Millionen von Partikeln bestehenden numerischen Modell. Eine Reduzierung auf den 2D-Fall mit Originalabmessungen und der Kornverteilung des Stückerzes reduziert die Modellgröße auf einige 100.000 Partikel. Aufgrund der zu modellierenden Echtzeit und der kleinen Partikelmassen kommt es bei der großen Partikelanzahl zu sehr hohen Rechenzeiten. Um diese zu reduzieren, wurde von der Modellsymmetrie Gebrauch gemacht. |
Um den Zeitschritt für die Integration der Bewegungsgleichungen zu vergrößern und damit die Anzahl von benötigten Rechenschritten für die Modellierung der benötigten Echtzeiten zu reduzieren, wurde ein Upscaling der Kornverteilung durchgeführt. Dazu wurden mehrere Versuchsrechnungen mit verschiedenen Upscaling-Faktoren durchgeführt, wobei ein Faktor von 7 als geeignet angesehen werden kann. Um zu einer weiteren Reduzierung der Rechenzeit zu gelangen, wurden die beiden kleinsten Kornklassen herausgenommen. Der Anteil der darüberliegenden Kornklasse wurde entsprechend erhöht. Diese Maßnahmen führen zu einem
2D-Modell mit insgesamt 5000 Partikeln und reduzieren die Rechenzeit
auf nur wenige Tage.
|
|
Der Bereich der Schneckenumhüllenden
ist durch vier Geraden begrenzt.
Die untere Grenze wird durch eine Wand dargestellt. Die
Auslaßfläche der Schnecke wird durch eine Aussparung
in der Schachtwand visualisiert, und die obere Begrenzung ist eine
imaginäre, nicht sichtbare Grenze,
deren Existenz nur durch das Verhalten der Partikel sichtbar wird. Die
rechte Begrenzung besteht ebenfalls aus einer Wand.
Bezüglich der Schneckenmodellierung wird folgende Strategie angewendet: Den Partikeln wird zunächst in einem schmalen Bereich eine Geschwindigkeit zugewiesen. Dieser Bereich, der nachfolgend als Abzugsbereich bezeichnet wird, ist durch zwei Geraden begrenzt, die parallel oberhalb und unterhalb der oberen Begrenzung der Schneckenumhüllenden verlaufen. Die Partikel bewegen sich im Abzugsbereich mit einer konstanten Geschwindigkeit nach unten. Unterhalb des Abzugsbereiches beginnt der Löschbereich, in welchen die Partikel nach Passieren des Abzugsbereiches gelangen und in kurzen Zeitabständen gelöscht werden. Diese Zeitabstände müssen so gewählt werden, daß sich der Löschbereich nicht vollständig mit Partikeln füllen kann und dadurch den Abzug beeinflußt. Im folgenden Abschnitt werden beispielhaft
einige
Abbildungen der Ergebnisse dargestellt:
Die Ergebnisse der Berechnungen zeigen u.a. den Effekt, daß sich
unter bestimmten Bedingungen eine partielle Entmischung
des Schüttgutes einstellt. Wann und in welchem Ausmaß eine
Entmischung auftritt, hängt dabei von mehreren Faktoren ab.
In der Abbildung 3 ist als Beispiel die Verteilung des Erzes zu einem bestimmten Zeitpunkt im Schacht dargestellt. Die Neigung des Spinnenbeines wird in diesem Fall variiert. Es zeigt sich, daß dieser Faktor einen wesentlichen auf die partielle Entmischung des Schüttgutes hat. Die Partikel wurden in diesem Fall nach Kornklassen eingefärbt um die Verteilung der Partikel besser darstellen zu können. |
|
|
Weiterhin ist es mit PFC
möglich die Spuren ausgewählter Partikel zu verfolgen (Abb.
4a)
oder die Kontaktkräfte zwischen den Partikel und den Partikeln und
den Wänden (Abb. 4b) darzustellen, um somit die gewonnenen
Ergebnisse zu verstehen und exakter beurteilen zu können.
Die Ergebnisse der Arbeit haben gezeigt, daß es mit PFC möglich ist Effekte nachzubilden und Einflüsse bezüglich des Fließverhaltens des Schüttgutes darzustellen. So konnte u.a. in den Simulationen erkannt werden, welche Einflüsse für die partielle Entmischung des Erzes verantwortlich sind. Weitere Details und die exakten Ergebnisse der können in der Diplomarbeit nachgelesen werden oder in der Publikation die im Tagungsband des 17. CADFEM Users' Meetings erschienen ist! |
|
Weitere Informationen...
|
|
...zu dieser Arbeit:
|
|
Fragen, ein Feedback oder Anregungen
können an A. J. Kleier
oder Herrn
|
|
...zu Themengebieten der numerischen
Simulation:
|
|
An der Technischen Fachhochschule Berlin
besteht die Möglichkeit den postgradualen Masterstudiengang
Computational Engineering zu
absolvieren. Studenten der TFH haben zudem die Möglichkeit zwei Lehrveranstaltungen zu besuchen,
die sich mit dem der Finiten Elemente Methode (FEM)
beschäftigen.
|
|
...zu Diplomarbeiten:
|
|
Bezüglich Diplomarbeiten die sich mit
numerischer Simulation befassen
ist Herr
|