Result. Math. 50 (2007) 109-124
Stephanie Müller
Angela Schwenk
Udo Simon
Eigenvalue equations in curve theory
Part II: Evolutes and Involutes
In the following are some illustrations referring to the article.
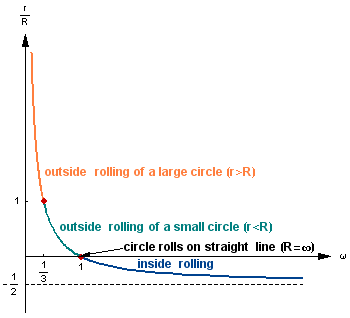
- Relation between ω and ratio of radii r/R
- Illustrations of the homethty between the involute and the evolute
- epicycloid
- hypocycloid
- logarithmic spiral d=-1
- logarithmic spiral: involute and evolute belong to the same curve
- superposition of two logarithmic spirals
- Illustrations of the spherical parametrization
- Familiy of involutes
1 Introduction
Local Classification.
Relation between ω and ratio of radii r/R defining the art of cycloids as mentioned in part A.1., A.2. and A.3.
![]()
First Equivalence Theorem
(iii) There exists p0 that an appropriate involute of the curve c and the evolute of the c are homothetic with respect to p0.
 d=ω2 > 0, 1/3 < ω < 1
d=ω2 > 0, 1/3 < ω < 1
Example: ω=3/5, hence r/R=1/3 .
The curve (red) is an arc of an epicycloid, its involute (blue) and its evolute (green) are homothetic with repect to the center of the fixed circle (black).
The dashed lines demonstrate the homothety, the factor of shortening is d=ω2=9/25.
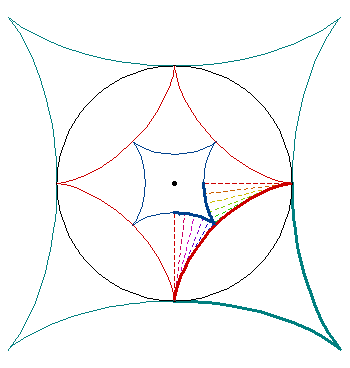 d=ω2 > 0, ω > 1
d=ω2 > 0, ω > 1
Example: ω=2, hence r/R=-1/4 .
The curve (red) is an arc of an hypocycloid, its involute (blue) and its evolute (green) are homothetic with repect to the center of the fixed circle (black).
The dashed lines demonstrate the relation between the curve and its involute. The homothety between the involute and evolute of c has a dilation factor of d=ω2=4.
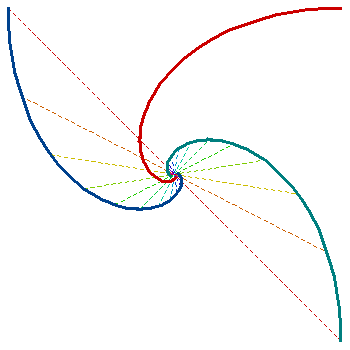 d=-ω2 < 0
d=-ω2 < 0
Example: d=-1 .
Here the curve (red) is a logarithmic spiral, its involute (blue) and its evolute (green) are homothetic with repect to intersection of the dashed lines.
The distance of c from the center is c=k exp(ω σ), for some constant k.
Due to d=-1, the dashed lines demonstrate the pure inversion without dilation or shortening between the involute and the evolute of c.
 d=-ω2 < 0
d=-ω2 < 0
Example: ω=-0.474541, this is a nice special case, where ω ist the solution of
Again the curve c (red) is a logarithmic spiral and, its involutec (blue) and its evolutec (green) are homothetic. The distance of c from the center is
Due log(ω2) = π ω the involute and evolute of c belong to the same spiral (shift of the parameter only by π):
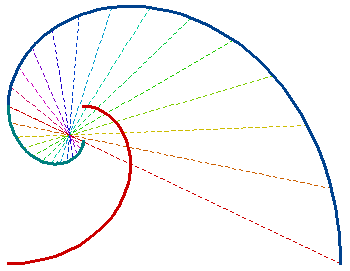
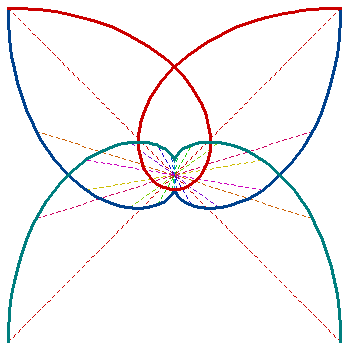 Superposition of two logarithmic spirals with d=-1 < 0;
Superposition of two logarithmic spirals with d=-1 < 0;
ω=-1 and ω=1 , radius of curvature κ = cosh(σ)
The curve (red) is a superposition of two logarithmic spirals with ω=-1 and ω=1, its involutec (blue) and its evolutec (green) are homothetic by an invesion.
The parametrization is given by 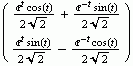 .
.
3 Examples
All examples use the spherical parametrization. The parameter intervall is divided into equidistant parts. Black dots mark the correspoding parts on the curve. It is then demonstrated, that the corresponding tangent vectors move unifomly along the sperical image.
 Cycloid
Cycloid
![]() , 0 < σ < π .
, 0 < σ < π .
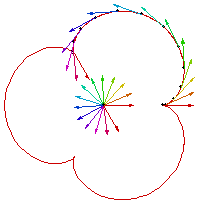 Epicycloid
Epicycloid
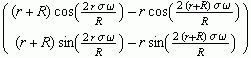 , 0 < σ < π/ω
, 0 < σ < π/ω
where ω=![]() =
=![]()
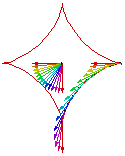 Hypocycloid
Hypocycloid
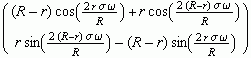 , 0 < σ < π/ω
, 0 < σ < π/ω
where ω=![]() =
=![]()
5 Involutes
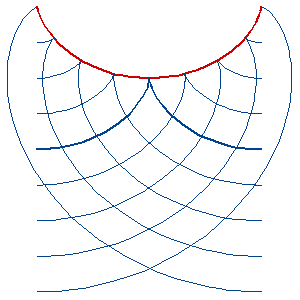
Family of involutes (blue) of a cycloid (red), which are optained by varying the parameter s1.
Choosing the right value of the parameter s1, gives again an cycloid (blue, thick), which differs by translation (see remark in 6.4 Proof of the First Equivalence Theorem).
The family of involutes of an arbitrary curve is always a family of parallel curves.