| © APSIS GmbH |
Seite 240
Seite 240
Seite 241
public static int maximaleTeilsumme3 (int[] folge) { // (11.1)
int summe, max = Integer.MIN_VALUE;
for (int von = 0; von < folge.length; von++)
for (int bis = von+1; bis < folge.length; bis++) { // Summe überprüfen
summe = 0;
for (int i = von; i <= bis; i++)
sume = summe + folge[i]; // ¬
if (max < summe) // Summe überprüfen, ob größer als die bisher größte
max = summe;
};
return max;
}
Übung 11.1: Ergänzen Sie das obige Programm durch Ausgaben (System.out.println) an verschiedenen Stellen, damit Sie seine Arbeitsweise nachvollziehen können. Führen Sie den Algorithmus mit 8 Zahlen auf Papier durch und vergleichen Sie Ihr Ergebnis mit der Ausgabe.
Seite 241
public static int maximaleTeilsumme2 (int[] folge) { // (11.2)
int[][] summen = new int[folge.length][folge.length];
// für i >= j ist summen[i][j] = Teilsumme i bis j = folge[i]+folge[i+1]+...+folge[j]
for (int i = 0; i < folge.length; i++)
for (int j = 0; j < folge.length; j++)
summen[i][j] = 0;
int max = Integer.MIN_VALUE;
summen[0][0] = folge[0]; // Teilsumme 0 .. 0
for (int bis = 1; bis < folge.length; bis++) // Teilsummen 0 .. 1, ..., 0 .. n-1
summen[0][bis] = summen [0][bis – 1] + folge[bis];
// auf die vorherige Teilsumme wird das nächste Element addiert
for (int von = 1; von < folge.length; von++)
for (int bis = von; bis < folge.length; bis++)
summen[von][bis] = summen[von - 1][bis] - folge[von – 1];
// Teilsumme fängt um ein Element nach rechts an: um dieses Element kleiner
// Tabelle summen wurde gefüllt; jetzt kann das maximale Element gesucht werden:
for (int von = 0; von < folge.length; von++) // ¬
for (int bis = 0; bis < folge.length; bis++)
if (max < summen[von][bis]) // überprüfen ob größer als die bisher größte
max = summen[von][bis];
if (folge.length == 0)
return 0; // die Summe der leeren Teilfolge ist 0
else
return max;
}
Übung 11.2: Ergänzen Sie die Programme (11.1) und (11.2) auf Seite 241 durch Zähler an verschiedenen Stellen im Programm. Weisen Sie das kubische bzw. quadratische Wachstum des Zeitaufwands durch Ausgabe der Zählerwerte für unterschiedlich große Folgen nach.
Seite 242
Seite 243
public static int fak(final int n) { // (11.3)
if (n == 1)
return 1;
else
return n * fak(n-1); // ¬
}
Übung 11.3: Unter Permutationen verstehen wir alle (unterschiedlichen) Umordnungen einer Menge; z.B. alle Permutationen von 123 sind 123 132 213 231 312 321. Die Anzahl der Permutationen aus n Elementen ist n! (n! ist die mathematische Bezeichnung der Fakultät, des Produkts der ersten n natürlichen Zahlen). Dies ist durch die folgende Überlegung, genannt mathematische Induktion, einleuchtend. Angenommen, wir haben alle Permutationen aus n-1 Elementen. Daraus erzeugen wir die Permutationen aus n Elementen, indem wir die Permutationen aus n-1 Elementen n-mal kopieren. Das n-te Element wird nun in der ersten Kopie vor das erste Element geschoben, in der zweiten vor das zweite, usw.; in der n-1-sten Kopie vor das n-1-ste (also das letzte) Element, schließlich in der n-ten Kopie nach dem letzten Element. Wenn die Anzahl der Permutationen aus n-1 Elementen Pn-1 war, dann erhalten wir auf diese Weise n .Pn-1 verschiedene Permutationen. Für n=1 ist diese Anzahl 1. Wenn Pn-1 = (n-1)!, dann Pn = n .Pn-1 = n .(n-1)! = n!.
Entwickeln Sie nun eine Funktion für die rekursive Berechnung von Permutationen. In der rekursiven Funktion permutationen sollen Sie eine lokale Reihung anlegen, die die Permutationen aus n-1 Elementen enthält. Sie sollen diese in das Ergebnis (ebenfalls eine lokale zweidimensionale Reihung der Größe n! .n, ) n-mal kopieren und das letzte Element an die 1-ste, 2-te, ... n-te Stelle einschieben. Eine geschickte Manipulation der Indizes ist hier der Schlüssel für eine elegante Lösung.
Fertigen Sie zwei Testtreiber für Ihre Klasse an: einen Stapeltesttreiber, der eine Reihung aus char-Elementen permutiert, sowie einen Dialogtesttreiber, der für eine eingegebene n die Ganzzahlen von 1 bis n permutiert.
Seite 244
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
| fn | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | ... |
Abb. 11.1: Fibonacci-Zahlen
public static int fibRek(final int n) { // (11.4)
if (n <= 0)
return 0;
else if (n == 1)
return 1;
else
return fibRek(n-1) + fibRek(n-2); // ¬
}
public static int fibIter(final int n) { // (11.5)
if (n > 0) {
int aktuelle = 1, hilfe = 1, vorherige = 0;
for (int i = 1; i < n; i++) { // ¬
hilfe = aktuelle;
aktuelle = aktuelle + vorherige;
vorherige = hilfe;
}
return aktuelle;
} else
return 0;
}
final int MAX = 10000; // (11.6)
long[] gedaechtnis = new long[MAX]; // ¬
for (int i = 0; i < gedaechtnis.length; i++) gedaechtnis[i] = 0; // vorbesetzen
long fib(final int n) throws UeberlaufAusn {
if (n > MAX) // wurde zu groß
throw new UeberlaufAusn();
else if (gedaechtnis[n] != 0) // schon errechnet
return gedaechtnis[n];
else if (n < 2) { // 0 oder 1
gedaechtnis[n] = n;
return gedaechtnis[n];
}
else
gedaechtnis[n] = fib(n-1) + fib(n-2); // rekursiv ¬
return gedaechtnis[n];
}
Übung 11.4: Erstellen Sie eine (rekursive) Funktionsdeklaration, die die Werte der Ackermann-Funktion liefert. Sie wird durch die folgende Formel definiert:
ackermann(n, m) = = n+1 wenn m = 0 = ackermann(m-1, 1) wenn m > 0 und n = 0 = ackermann(m-1, ackermann (m, n-1)) ansonsten
Schreiben Sie ein Testprogramm für diese Funktion. Überwachen Sie die Laufzeit des Funktionsaufrufs mit Hilfe Methode getTime der Klasse java.util.Date (diese parameterlose Funktion liefert einen long-Wert, die Anzahl der Millisekunden seit dem 1. Januar 1970, 0 Uhr GMT). Ermitteln Sie auch die Anzahl der rekursiven Aufrufe und stellen Sie eine Tabelle für verschiedene Parameterkombinationen zusammen.
Die Ackermann-Funktion ist ein Beispiel für eine Rekursion, die nicht (oder zumindest nicht direkt) durch Iteration ersetzt werden kann. Ihre Eigenschaft ist bekannt, dass sie stärker wächst als jede sog. primitiv-rekursive Funktion: Der Wert von ackermann(4, 2) kann mit 19729 Dezimalziffern beschrieben werden. ackermann(4, 4) ist größer als 10N, wo N = 10M, wo M = 1019000. (Die Anzahl der Elementarteilchen im bekannten Universum liegt etwa bei 1070.)
Übung 11.5: Erstellen Sie eine Klasse, deren Exportfunktion die Werte der Ackermann-Funktion mit Hilfe eines Gedächtnisses liefert. Modifizieren Sie das Testprogramm aus der vorherigen Aufgabe dafür. Lesen Sie die Parameterwerte der Funktion von der Kommandozeile über den Parameter args der main-Methode ein: zusammen mit dem Aufruf des Programms aus dem Betriebssystem heraus (s. im Kapitel 9.2.4. auf Seite 199).
Seite 245
Abb. 11.2: Türme von Hanoi
void uebertragen(int n, final String a, final String b, final String c) { // (11.7)
// überträgt n Scheiben von a nach b mit Hilfe von c
if (n > 0) {
uebertragen(n-1, a, c, b); // ¬
System.out.println("Übertragung vom " + a + " nach " + b);
uebertragen(n-1, c, b, a); // ¬
}
}
void hanoi(int anzahl) {
uebertragen(anzahl, "ersten", "zweiten", "dritten");
}
Seite 246
class SortierBaum { // (11.8)
protected BaumElement wert; // geordnete Klasse mit Rückrufmethode uebernehmen
protected SortierBaum links, rechts; // links enthält kleinere, rechts größere Werte
public SortierBaum(BaumElement wert) { this.wert = wert; }
public void aufbau(BaumElement element) {
if (element.kleiner(wert)) { // BaumElement-Rückruf
if (links == null)
links = new SortierBaum(element); // neuer Baum
else
links.aufbau(element); // rekursiv
} else { ... // rechts ähnlich
}
public void abbau() {
if (links != null)
links.abbau();
wert.uebernehmen(); // Rückrufmethode ¬
if (rechts != null)
rechts.abbau();
}
}
class BaumSort extends SortierBaum {
public BaumSort(BaumElement [] elemente) { // Elemente in einer Reihung
super(elemente[0]); // Wurzel erzeugen
for (int i = 1; i < elemente.length; i++) // vom zweiten Element an
aufbau(elemente[i]);
abbau(); // uebernehmen von BaumElement wird mit sortierten Elementen aufgerufen
}
}
class GanzElement implements BaumElement {
int wert;
public GanzElement(int wert) { this.wert = wert; }
public boolean kleiner(final BaumElement element) {
return wert < ((IntegerElement)element).wert;
}
public void uebernehmen() {
System.out.println(wert);
}
}
GanzElement[] elemente; ... // elemente erzeugen und mit Ganzzahlwerten auffüllen new BaumSort(elemente); // Inhalt von elemente wurde sortiert ausgegeben
Übung 11.6: Ergänzen Sie das obige Programm durch Ausgaben (System.out.println) an verschiedenen Stellen, damit Sie seine Arbeitsweise nachvollziehen können. Führen Sie den Algorithmus mit 20 Zahlen auf Papier durch und vergleichen Sie Ihr Ergebnis mit der Ausgabe.
Seite 248
Seite 248
public class BlasenSort { // (11.9)
public BlasenSort(Element[] daten) { // bubble sort
// Idee: benachbarte Elemente austauschen, wenn das größere vorne liegt
for (int i = 0; i < daten.length; i++) // oft genug wiederholen ¬
for (int j = 0; j < daten.length-1; j++) // ¬
if (daten[j+1].kleiner(daten[j])) { // vergleichen
final Element temp = daten[j+1]; // austauschen
daten[j+1] = daten[j];
daten[j] = temp;
}
}
}
5 1 3 6 8 2 7 4 5 1 3 6 2 8 7 4 5 1 3 6 2 7 8 4 5 1 3 6 2 7 4 8 1 5 3 6 2 7 4 8 1 3 5 6 2 7 4 8 1 3 5 2 6 7 4 8 1 3 5 2 6 4 7 8 1 3 2 5 6 4 7 8 1 3 2 5 4 6 7 8 1 2 3 5 4 6 7 8 1 2 3 4 5 6 7 8
public direktesEinfuegen(Element[] daten) { // straight insertion // (11.10)
/* Idee: Das index-te Element (von der zweiten Stelle an bis nach daten.length-1) wird
in die schon sortierte Teilsequenz 1 .. index-1 eingefügt. Die Einfügestelle wird in
der Teilsequenz 1 .. index-1 gesucht und dabei wird jedes Element nach hinten
geschoben. */
for (int index = 1; index < daten.length; index++) { // von der zweiten Stelle an
final Element elZumEinfuegen = daten[index];
int einfuegestelle = index;
// in der sortierten Teilsequenz 1 .. index-1 Einfügestelle suchen:
while (einfuegestelle > 0 && elZumEinfuegen.kleiner(daten[einfuegestelle-1])) { // ¬
daten[einfuegestelle] = daten[einfuegestelle-1]; // hochschieben ¬
einfuegestelle --; // weitergehen nach unten
}; // Einfügestelle gefunden: entweder weil einfuegestelle = 0
// oder weil elZumEinfuegen.nichtKleiner(daten[einfuegestelle – 1])
daten[einfuegestelle] = elZumEinfuegen;
}
}
5 > 6 1 3 8 2 7 4 > 5 6 1 3 8 2 7 4 1 > 5 6 3 8 2 7 4 1 3 5 6 > 8 2 7 4 1 > 3 5 6 8 2 7 4 1 2 3 5 6 > 8 7 4 1 2 3 > 5 6 7 8 4 1 2 3 4 5 6 7 8
Übung 11.7: Verbessern Sie den Blasensort, indem Sie durch die geschachtelte Schleife nicht immer unbedingt n2 mal durch die Reihung laufen, sondern abbrechen, nachdem kein Austausch mehr stattgefunden hat.
Übung 11.8: Eine weitere Verbesserung von Blasensort ist Schüttelsort (shaker sort). Hier wird die Durchlaufrichtung abwechselnd geändert: Nachdem eine "leichte Blase" aufwärts gestiegen ist, steigt eine "schwere Blase" nach unten. Programmieren Sie das Verfahren und zeigen Sie die schrittweise Veränderungen einer Zufallsfolge aus Ganzzahlen am Bildschirm an.
Übung 11.9: Verbessern Sie das direkte Einfügen im Programm (11.10) auf Seite 249 um das binäre Suchen, in dem die Suche nach der Einfügestelle in der sortierten Teilsequenz nicht sequenziell erfolgt, sondern durch wiederholtes Halbieren der Sequenz:
while (links <= rechts) { // binäres Suchen in der sortierten Teilsequenz // (11.11)
final int mitte = (links + rechts) / 2;
if (elZumEinfuegen.kleiner(daten[mitte])) // vergleichen ¬
rechts = mitte-1;
else
links = mitte+1;
} // Einfügestelle gefunden: links
Übung 11.10: Programmieren Sie das direkte Auswählen (straight selection): In jedem Schritt wird das kleinste Element gefunden und mit dem untersten unsortierten ausgetauscht. In der schrittweisen Darstellung der Veränderungen unserer Zufallsfolge haben wir das kleinste unsortierte Element fett gedruckt, den untersten unsortierten (mit dem es ausgetauscht wird) unterstrichen:
5 6 1 3 8 2 7 4 1 6 5 3 8 2 7 4 1 2 5 3 8 6 7 4 1 2 3 5 8 6 7 4 1 2 3 4 8 6 7 5 1 2 3 4 5 6 7 8
Seite 250
public shellSort(Element[] daten, int[] k) { Schrittweiten in k // (11.12)
for (int m = 0; m < k.length; m++) {
// in jedem Durchlauf ein k[m]-Sort
int k = k[m]; // aktuelle Schrittweite
// direktes Einfügen mit Schrittweite k: ¬
for (int index = k; index < daten.length; index++) { // Schleife des k-Sorts
Element elZumEinfuegen = daten[index];
int einfuegestelle = index;
while (einfuegestelle - k >= 0 &&
elZumEinfuegen.kleiner(daten[einfuegestelle – k])) {
daten[einfuegestelle] = daten[einfuegestelle – k];
einfuegestelle = einfuegestelle - k; // nächstes Element zu vergleichen
}
daten[einfuegestelle] = elZumEinfuegen;
}
}
}
5 6 1 3 8 2 7 4 (Schrittweite 7) 4 6 1 3 8 2 7 5 (Schrittweite 3) 3 6 1 4 8 2 7 5 3 5 1 4 6 2 7 8 (Schrittweite 1) 1 3 5 4 6 2 7 8 ... (usw., direktes Einfügen)
Übung 11.11: Ergänzen Sie das obige Programm (11.12) auf Seite 250 durch Ausgaben (System.out.println) an verschiedenen Stellen, damit Sie seine Arbeitsweise nachvollziehen können. Führen Sie den Algorithmus mit 20 Zahlen auf Papier durch und vergleichen Sie Ihr Ergebnis mit der Ausgabe.
Seite 251
public class SchnellSort { // quick sort // (11.13)
private Element[] daten;
private void sort(int links, int rechts) {
int auf = links; // linke Grenze
int ab = rechts; // rechte Grenze
final Element mitte = daten[(links + rechts) / 2]; // mittleres Element
do {
while (daten[auf].kleiner(mitte))
auf ++; // suchen größeres Element von links
while (mitte.kleiner(daten[ab]))
ab --; // suchen kleineres Element von rechts
if (auf <= ab) { // austauschen auf und ab:
Element temp = daten[auf];
daten[auf] = daten[ab];
daten[ab] = temp;
auf ++; // linke und rechte Grenze verschieben:
ab --;
};
} while (auf <= ab); // Überschneidung
if (links < ab)
sort(links, ab); // sortiere linke Hälfte ¬
if (auf < rechts)
sort(auf, rechts); // sortiere rechte Hälfte ¬
}
public SchnellSort(Element[] daten) {
this.daten = daten;
sort(0, daten.length-1); // sortiere die ganze Sequenz ¬
}
}
5 6 1 3 8 2 7 4 2 6 1 3 8 5 7 4 2 3 1 | 6 8 5 7 4 2 1 | 3 | 6 8 5 7 4 1 2 3 | 6 8 5 7 4 1 2 3 | 4 8 5 7 6 1 2 3 | 4 5 | 8 7 6 1 2 3 | 4 5 | 6 7 8
public class HaldenSort { // heap sort // (11.14)
private Element[] daten; // daten[0] ungenutzt
/* Der Reihungsausschnitt daten[a .. b] erfüllt die Haldenbedingung, wenn für jedes
i mit 2*i+1 <= b gilt: daten[i] > daten[2*i] && daten[i] > daten[2*i+1] */
private void senken(final int links, final int rechts) {
/* Die Halde daten[links .. rechts] wird durch das Senken des Elements
daten[links – 1] zur Halde daten[links - 1 .. rechts] erweitert. */
int index = links - 1; // linke Grenze der neuen Halde
int nachfolger = 2 * index; // linker Nachfolger
final Element elementZuSenken = daten[index];
while (true) { // rumpfgesteuerte Schleife mit zwei Abbruchstellen
if (nachfolger > rechts) break; // weil Nachfolger nicht existiert
if (nachfolger < rechts && daten[nachfolger].kleiner(daten[nachfolger + 1]))
// kleineren nachfolger oder nachfolger + 1 auswählen
nachfolger ++;
if (daten[nachfolger].kleiner(elementZuSenken)) break; // Platz gefunden ¬
daten[index] = daten[nachfolger]; // hochrücken
index = nachfolger; // nach unten gehen
nachfolger = 2 * index; // linker Nachfolger, wenn existiert
};
daten[index] = elementZuSenken; // Element einfügen
}
public HaldenSort(Element[] daten) {
this.daten = daten;
/* Halde aufbauen (die obere Hälfte daten[daten.length/2+1 .. daten.length-1])
erfüllt die Haldenbedingung immer): */
int rechts = daten.length-1;
for (int links = rechts / 2 + 1; links > 1; links--)
// die untere Hälfte einzeln zur Halde hinzufügen
senken(links, rechts); // ¬
// jetzt erfüllt die Reihung daten[1 .. daten.length-1] die Haldenbedingung
// Halde abbauen = Reihung sortieren:
final int links = 1; // daten[0] ungenutzt
for (rechts = daten.length-1; rechts > links; rechts--) {
// austauschen der äußeren Elemente:
Element groesstesElement = daten[links]; // Spitzenelement der Halde
daten[links] = daten[rechts]; // hinteres Element nach vorne
daten[rechts] = groesstesElement; // sortiertes Element nach hinten
senken(links + 1, rechts - 1); // neues Element in der Halde senken ¬
}
}
}
5 6 1 3 > 8 2 7 4 < 5 6 1 > 4 8 2 7 3 < 5 6 > 7 4 8 2 1 3 < 5 > 8 7 4 6 2 1 3 < > 8 6 7 4 5 2 1 3 < Halde fertig > 7 6 3 4 5 2 1 < 8 > 6 5 3 4 1 2 < 7 8 > 5 4 3 2 1 < 6 7 8 > 4 2 3 1 < 5 6 7 8 > 3 2 1 < 4 5 6 7 8 > 2 1 < 3 4 5 6 7 8 > 1 < 2 3 4 5 6 7 8
Übung 11.12: Ergänzen Sie die obigen Programme (11.13) auf Seite 251 und (11.14) auf Seite 253 durch Ausgaben (System.out.println) an verschiedenen Stellen, damit Sie seine Arbeitsweise nachvollziehen können. Führen Sie die Algorithmen mit 20 Zahlen auf Papier durch und vergleichen Sie Ihre Ergebnisse mit der Ausgabe.
Übung 11.13: Ergänzen sie den Algorithmus HaldenSort durch die Prüfung der Haldenbedingung nach jedem Austausch (hierdurch wird die Zeitkomplexität des Algorithmus O(n2), daher ist dieser Einschub nur zu Testzwecken zu verwenden). Geben Sie die Sequenz nach jedem Austausch aus. Aktivieren Sie ihn in einem Testtreiber, in dem acht Ganzzahlen sortiert werden. Identifizieren Sie in jeder ausgegebenen Sequenz die Halde und die sortierte Teilsequenz.
Übung 11.14: Für das Mischen (wie im Kapitel 10.3.6. auf Seite 235 vorgestellt) braucht man möglichst lange sortierte Teilsequenzen. Die maximale Durchschnittslänge von ca. 2n, die in einer Reihung mit gegebener Länge n erreicht werden kann, ergibt folgende Strategie:
Programmieren Sie dieses Verfahren. Sortieren Sie in einem Testtreiber ca. 1000 Zufallszahlen in einer Reihung der Länge 100 und prüfen Sie, ob sie wirklich in ca. 5 Teilsequenzen sortieren lassen.
Übung 11.15: Programmieren Sie den Multibehälter SortierKanalGen aus dem Kapitel 8.3.9. auf Seite 190 als ein fortschrittlicher Haldensortalgorithmus.
Seite 255
/* Jede Sortierprozedur, die sich für die Messung qualifizieren will, muss // (11.15)
SortTest erweitern und die aufgeschobene Methode sortieren überschreiben.
Sie kann dabei die Methoden datenlaenge, vergleichen und austauschen aufrufen.
In main soll die Methode sort (parametrisiert mit den zu sortierenden Daten)
aufgerufen werden; sie liefert ein Objekt der Klasse Ergebnis. */
final class Ergebnis implements Cloneable {
public long vergleiche, austausche; // Ergebnisse der Messung
public void Ergebnis() {
vergleiche = 0; austausche = 0;
}
public Object clone() {
try {
return super.clone();
} catch (CloneNotSupportedException ausnahme) { // darf nicht auftreten
System.err.println(ausnahme);
return null;
}
}
}
abstract class SortMessung { // Klasse für Messen von Sortierverfahren
private double[] werte;
private Ergebnis ergebnis = new Ergebnis(); // setzt Messdaten auf 0
// geschützte Schnittstelle:
protected abstract void sortieren(); // wird überschrieben
protected final int datenlaenge() {
return werte.length;
}
protected final boolean vergleichen(int i, int j) { // für Rückruf
ergebnis.vergleiche ++;
return werte[i] < werte[j];
}
protected final void austauschen(int i, int j) { // für Rückruf
ergebnis.austausche ++;
double temp = werte[i];
werte[i] = werte[j];
werte[j] = temp;
}
// öffentliche Schnittstelle:
public final Ergebnis sort(double[] sortierdaten) {
werte = sortierdaten;
sortieren(); // Aufruf des aufgeschobenen Sortieralgorithmus
return (Ergebnis)ergebnis.clone(); // Kopie des Ergebnisses, keine Referenz! ¬
}
}
class BlasenSortMessung extends SortMessung { // Blasensort // (11.16)
protected void sortieren() {
for (int i = 0; i < datenlaenge(); i++)
for (int j = 0; j < datenlaenge(); j++)
if (vergleichen(i, j))
austauschen(i, j);
}
Übung 11.16: Gestalten Sie die folgenden Sortierverfahren so um, dass sie sich für SortMessung qualifizieren:
Versorgen Sie die Aufrufe mit einer Reihung von 20 zufälligen int-Werten und vergleichen Sie die Messergebnisse.
Übung 11.17: Weisen Sie die Komplexitätsformel O(n2) mit Hilfe der Programme aus der vorherigen Übung auf Seite 256 nach: Zeigen Sie, dass eine doppelt, dreifach, ... zehnfach lange Sequenz ungefähr viermal, neunmal, ... hundertmal so viele Vergleiche bzw. Austausche braucht, um mit einem quadratischen Verfahren sortiert zu werden. Eine Verbesserung des Verfahrens (wie etwa Schüttelsort gegenüber Blasensort oder binäres Einfügen gegenüber direktem Einfügen) ergibt zwar bessere Messergebnisse, das Verhältnis wird aber nicht verändert.
Zeigen Sie auch, dass bei höheren Verfahren (z.B. beim Schnellsort) das Wachstum deutlich unter n2 bleibt.
Seite 257
interface Element { // (11.17)
public boolean kleiner(final Element element); // vergleicht zwei Elemente
// requires a.kleiner(b) | b.kleiner(a) | a.gleich(b);
void rueckruf(); // für die Iteratoren
}
interface Baum { // (11.18)
public void eintragen(final Element element); // sortiert element in den Baum ein
// ensures vorhanden(element);
public void loeschen(final Element element); // löscht element aus dem Baum
public boolean vorhanden(final Element element); // const
public void iteratorPre(); // Präorder ¬
public void iteratorIn(); // Inorder
public void iteratorPost(); // Postorder
}
Seite 258
public class BaumImpl implements Baum { // (11.19)
private Element wert; private Baum links, rechts; // links enthält kleinere, rechts größere Werte
public BaumImpl(Element wert) { this.wert = wert; } public void eintragen(final Element element) { ... // s. aufbau im Programm (11.8)
public boolean vorhanden(final Element element) {
if (element.kleiner(wert))
return links == null || links.vorhanden(element); // kurzgeschlossen
else if (wert.kleiner(element))
return rechts == null || rechts.vorhanden(element);
else // wert.gleich(element)
return true;
}
public void iteratorIn() {
if (links != null)
links.iteratorIn();
wert.rueckruf();
if (rechts != null)
rechts.iteratorIn();
}
... // andere Iteratoren ähnlich: rueckruf vor bzw. nach den rekursiven Aufrufen
}
Übung 11.18: Programmieren Sie die Informatoren
Element kleinstesElement(); // liefert das kleinste Element im Baum Element groesstesElement(); // liefert das größte Element im Baum
sowohl rekursiv wie auch mit Wiederholung.
Übung 11.19: Ergänzen Sie das Programm (11.19) durch Ausgaben. Tragen Sie 20 Zahlen auf Papier in den Baum ein und vergleichen Sie Ihre Ergebnisse mit der Ausgabe.
Rufen Sie im Testtreiber – nachdem Sie den Baum aufgebaut haben – auch die drei Iteratoren auf; in der Rückrufmethode (der Elementklasse) sollen sie das Element auf System.out ausgeben und erklären Sie das Ergebnis.
Seite 259
public class LBaum implements Baum { // löschbarer Baum // (11.20)
private class Knoten {
Element wert;
LBaum links, rechts;
Knoten(Element wert) { // ensures links != null && rechts != null
this.wert = wert;
links = new LBaum();
rechts = new LBaum();
}
}
private Knoten knoten; // LBaum ist parameterlos konstruierbar
public void eintragen(final Element element) {
if (knoten == null) // Baum ist leer
knoten = new Knoten(element);
else if (element.kleiner(knoten.wert))
knoten.links.eintragen(element);
else // rechts eintragen, auch wenn gleich
knoten.rechts.eintragen(element);
}
public void iteratorIn() {
if (knoten != null) {
knoten.links.iteratorIn();
knoten.wert.rueckruf();
knoten.rechts.iteratorIn();
}
}
... // andere Iteratoren ähnlich; vorhanden wie im Programm (11.19), jedoch
// knoten.wert statt wert, knoten.links statt links, knoten.rechts statt rechts
Fall 1 |
Fall 2 |
Fall 3 |
kein Nachfolger: löschen |
ein Nachfolger: umhängen |
zwei Nachfolger: |
Abb. 11.3: Löschen im Binärbaum
public void loeschen(final Element element) { // (11.21)
if (knoten == null) // Baum ist leer
return; // element ist nicht vorhanden
else if (element.kleiner(knoten.wert))
knoten.links.loeschen(element); // suchen links
else if (knoten.wert.kleiner(element))
knoten.rechts.loeschen(element); // suchen rechts
// else element.gleich(knoten.wert) // Element gefunden
else if (knoten.links.knoten == null) { // höchstens ein Nachfolger
if (knoten.rechts.knoten == null) // kein Nachfolger: Fall (1)
knoten = null; // gefundenen Knoten vernichten
else // ein Nachfolger: rechts; Fall (2)
knoten = knoten.rechts.knoten; // rechten Teilbaum einhängen
}
else if (knoten.rechts.knoten == null) // ein Nachfolger: links; Fall (2)
knoten = knoten.links.knoten; // linken Teilbaum einhängen
// else zwei Nachfolger: Fall (3)
/* das kleinste Element im rechten (größeren) Teilbaum wird mit dem gefundenen
Element ausgetauscht, dann gelöscht: */
else if (knoten.rechts.knoten.links.knoten == null) {
// rechts hat keinen linken Nachfolger: rechts kopieren und aushängen
knoten.wert = knoten.rechts.knoten.wert; // Inhalt kopieren
knoten.rechts = knoten.rechts.knoten.rechts; // rechts aushängen
} else { // kleinstes Element suchen, austauschen und löschen:
LBaum vaterDesKleinsten = knoten.rechts.vater();
LBaum kleinster = vaterDesKleinsten.knoten.links;
// kleinster hat höchstens einen (rechten) Nachfolger
this.knoten.wert = kleinster.knoten.wert; // Inhalt kopieren
vaterDesKleinsten.loeschen(kleinster.knoten.wert); // kleinsten Knoten löschen
}
}
private LBaum vater() {
// liefert den Baum, dessen linker Nachfolger den kleinsten Wert hat
if (knoten.links.knoten.links.knoten == null) // links hat keinen linken Nachfolger
return this;
else
return knoten.links.vater(); // rekursiv
}
Übung 11.20: Gestalten Sie Ihren Testtreiber aus der Übung 11.19 auf Seite 258 für die Klasse LBaum um. Nachdem Sie den Baum aufgebaut haben, löschen Sie alle Elemente nacheinander; rufen Sie nach jedem Löschen iteratorIn auf. Üben Sie den Algorithmus vorher auf Papier und vergleichen Sie Ihre Ergebnisse mit der Ausgabe.
Übung 11.21: Der dargestellte Löschalgorithmus ist auch für BaumImpl implementierbar, wenn die Klasse um eine Datenkomponente ergänzt wird, durch die jeder Knoten seinen Vaterknoten referiert. Dann kann ein gefundenes Element ausgehängt werden. Der Wurzelknoten muss allerdings immer gesondert behandelt werden.
Erweitern Sie nun die Klasse BaumImpl auf diese Weise und implementieren Sie darin loeschen. Der Testtreiber aus der vorherigen Übung auf Seite 261 soll hierfür – nach geeigneter Umgestaltung – auch funktionieren.
Seite 261
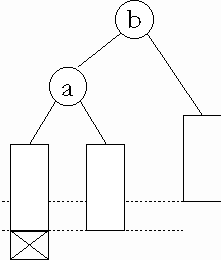
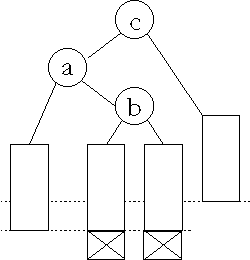
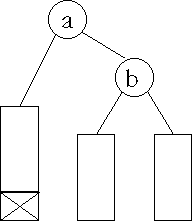
Einfaches Rotieren |
Doppeltes Rotieren |
 |
 |
 |
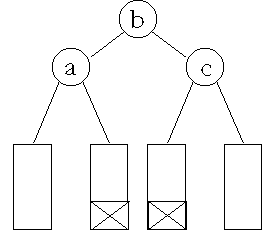 |
Abb. 11.4: Eintragen in einen AVL-Baum (nach [Wir], Seite 248)
public class ABaum { // ausgeglichener Baum; parameterlos konstruierbar // (11.22)
// Werte für ausgleich in der Knoten-Klasse:
protected final static int LINKS = -1; // linkslastig
protected final static int AUSG = 0; // ausgeglichen
protected final static int RECHTS = 1; // rechtslastig
private class Knoten {
Element wert;
ABaum links, rechts;
int ausgleich; // LINKS oder AUSG oder RECHTS ¬
int zaehler; // doppeltes Eintragen wird gezählt
Knoten(Element wert) { // ensures links != null && rechts != null
this.wert = wert; links = new ABaum(); rechts = new ABaum();
ausgleich = AUSG; zaehler = 1;
}
}
private Knoten knoten;
public ABaum() { knoten = null; } // öffentlicher Konstruktor
private ABaum(final ABaum quelle) { // privater Kopierkonstruktor
knoten = new Knoten(quelle.knoten.wert); knoten.zaehler = quelle.knoten.zaehler;
knoten.links = quelle.knoten.links; knoten.rechts = quelle.knoten.rechts;
}
protected int ausgleich = AUSG;
public boolean eintragen(Element element) {
// Ergebnis wird nur privat benutzt: ob Ast verlängert
boolean astVerlaengert = false;
if (knoten == null) // Baum ist leer
knoten = new Knoten(element);
else if (element.kleiner(knoten.wert)) { // Eintragen in links
if (knoten.links.knoten == null) { // Einfügestelle gefunden
knoten.links.knoten = new Knoten(element);
knoten.ausgleich --; // Baum wird linkslastiger
astVerlaengert = knoten.rechts.knoten == null;
} else {
astVerlaengert = knoten.links.eintragen(element); // rekursiv
if (astVerlaengert)
switch (knoten.ausgleich) {
case AUSG: // Ausgeglichenheit bleibt erhalten
knoten.ausgleich = LINKS; // Baum wird linkslastig
break;
case RECHTS: // Ausgeglichenheit bleibt erhalten
knoten.ausgleich = AUSG;
astVerlaengert = false;
break;
case LINKS: // Ausgeglichenheit wird verletzt, Rotieren nötig
if (knoten.links.knoten.ausgleich == RECHTS) // innen schwer:
doppeltesRotierenLinks();
else // außen schwer:
einfachesRotierenLinks();
knoten.ausgleich = AUSG;
astVerlaengert = false;
};
}
} else if (knoten.wert.kleiner(element)) { ... // symmetrisch für rechts
} else // Element im Baum vorhanden
knoten.zaehler ++;
return astVerlaengert;
}
private void einfachesRotierenLinks() {
final ABaum zweigB = new ABaum(this);
final ABaum zweigA = knoten.links;
final ABaum mittlererAst = zweigA.knoten.rechts;
knoten.wert = zweigA.knoten.wert; // der schwere Knoten wird zur neuen Wurzel
knoten.zaehler = zweigA.knoten.zaehler;
knoten.rechts = zweigB; // Knoten umhängen
knoten.links = zweigA.knoten.links;
knoten.ausgleich ++;
zweigB.knoten.links = mittlererAst; // mittleren Ast umhängen; äußere bleiben
zweigB.knoten.ausgleich = AUSG;
}
private void einfachesRotierenRechts() { ... } // symmetrisch
private void doppeltesRotierenLinks() {
final ABaum zweigC = new ABaum(this);
final ABaum zweigA = zweigC.knoten.links;
final ABaum zweigB = zweigA.knoten.rechts;
final ABaum linkerAst = zweigB.knoten.links; // schwerer Ast in der Mitte
final ABaum rechterAst = zweigB.knoten.rechts; // anderer Ast in der Mitte
knoten.wert = zweigB.knoten.wert; // schwerer Knoten wird Wurzel (hochziehen)
knoten.zaehler = zweigB.knoten.zaehler;
knoten.links = zweigA; // Knoten umhängen an die neue Wurzel
knoten.rechts = zweigC;
zweigA.knoten.rechts = linkerAst; // Äste in der Mitte umhängen
zweigC.knoten.links = rechterAst; // die äußeren Äste bleiben
if (zweigB.knoten.ausgleich == LINKS)
zweigC.knoten.ausgleich = RECHTS;
else
zweigC.knoten.ausgleich = AUSG;
zweigA.knoten.ausgleich --;
knoten.ausgleich = AUSG;
}
void doppeltesRotierenRechts() { ... } // symmetrisch
...
Übung 11.22: Ergänzen Sie das Programm (11.22) auf Seite 264 durch Ausgaben. Tragen Sie 20 Zahlen auf Papier in den AVL-Baum ein und vergleichen Sie Ihre Ergebnisse mit der Ausgabe.
Übung 11.23: Ergänzen Sie die Klasse ABaum mit einem zusätzlichen (rekursiven) Informator tiefe, der Tiefe eines Baums berechnet. Er soll auch die Differenz der Tiefen der beiden Teilbäume überprüfen und melden, falls sie größer als 1 ist. Er ist für den Nachweis der Richtigkeit des Algorithmus geeignet. Programmieren Sie einen Stapeltesttreiber main und geben Sie nach jedem Einfügen und nach jedem Löschen die Tiefe des Baums aus.
Seite 266
public boolean loeschen(final Element element) {
// Ergebnis wird nur privat benutzt: ob Ast gekürzt
boolean astGekuerzt = false;
if (knoten == null) ; // Baum ist leer: element ist nicht vorhanden
else if (element.kleiner(knoten.wert)) {
astGekuerzt = knoten.links.loeschen(element); // suchen links
if (astGekuerzt) astGekuerzt = linksAusgleichen();
}
else if (knoten.wert.kleiner(element)) { ... } // symmetrisch
else if (knoten.zaehler > 1) // element.gleich(knoten.wert) // element gefunden
knoten.zaehler --;
else { // zaehler == 1, Knoten soll gelöscht werden
if (knoten.links.knoten == null) { // kein linker Nachfolger
knoten = knoten.rechts.knoten; astGekuerzt = true;
} else if (knoten.rechts.knoten == null) { // kein rechter Nachfolger
knoten = knoten.links.knoten; astGekuerzt = true;
} else { // zwei Nachfolger
ABaum kleinster = // kleinster hat höchstens einen (rechten) Nachfolger
rechts.knoten.links.knoten == null ? // rechts kein linker Nachfolger
rechts.knoten.rechts :
knoten.rechts.vater().knoten.links;
knoten.wert = kleinster.knoten.wert; // Inhalt kopieren
knoten.zaehler = kleinster.knoten.zaehler;
kleinster.knoten.zaehler = 1; // kleinsten Knoten im rechten Zweig löschen
astGekuerzt = knoten.rechts.loesch(kleinster.knoten.wert);
if (astGekuerzt) astGekuerzt = rechtsAusgleichen();
}
}
return astGekuerzt;
}
private ABaum vater() { ... } // wie im Programm (11.21)
private boolean linksAusgleichen () { // linker Ast wurde kürzer
// Ergebnis: ob Ast gekürzt
boolean astGekuerzt = true;
int ausgleichRechts = AUSG;
if (knoten.rechts.knoten != null) ausgleichRechts = knoten.rechts.knoten.ausgleich;
switch (knoten.ausgleich) {
case LINKS: knoten.ausgleich = AUSG; break;
case AUSG: knoten.ausgleich = RECHTS; astGekuerzt = false; break;
case RECHTS: // Ausgleich nötig
switch(ausgleichRechts) {
case LINKS: doppeltesRotierenRechts(); break;
case AUSG: einfachesRotierenRechts();
knoten.links.knoten.ausgleich = RECHTS;
knoten.ausgleich = LINKS;
astGekuerzt = false;
break;
case RECHTS: einfachesRotierenRechts();
knoten.links.knoten.ausgleich = knoten.ausgleich = AUSG;
}
}
return astGekuerzt;
}
private void rechtsAusgleichen() { ... } // symmetrisch
Übung 11.24: Setzen Sie die Übung 11.22 auf Seite 266 fort, indem Sie die 20 Zahlen nacheinander aus dem AVL-Baum löschen. Ergänzen Sie auch Ihren Testtreiber durch geeignete Ausgaben (z.B. Aufruf von iteratorPre nach jedem loeschen), mit denen Sie Ihre Ergebnisse vergleichen können.
Übung 11.25: Die obigen Algorithmen verletzten einige der in diesem Lehrbuch vertretenen Prinzipien: Die Methoden sind lang und tief geschachtelt. Von Klassenerweiterung wird kein Gebrauch gemacht: Sie sind eher "klassisch" formuliert, um die Abläufe verständlich zu machen. Bauen Sie nun die Klassen LBaum und ABaum (einschließlich der Klasse Knoten) zu einer Klassenhierarchie mit möglichst kurzen, übersichtlichen Methodenrümpfen um.
Seite 267
Algorithmus |
Basis |
Zeitkomplexität |
Speicherkomplexität |
| Maximale Teilsumme (11.1) | M | kubisch | konstant |
| Maximale Teilsumme (11.2) | M | quadratisch | quadratisch |
| Fakultät iterativ (11.3) | G | linear | konstant |
| Fakultät rekursiv (Übung 10.1) | G | linear | linear |
| Fibonacci rekursiv (11.4) | G | exponenziell | logarithmisch |
| Fibonacci iterativ (11.5) | G | linear | linear |
| Fibonacci Gedächtnis (11.6) | G | linear | logarithmisch |
| Ackermann (Übung 11.4) | G | > exponenziell | > exponenziell |
| Türme von Hanoi (11.7) | G | exponenziell | logarithmisch |
| Binärbaum-Sort (11.8) | M | logarithmisch (entartet: linear) |
linear |
| Blasensort (11.9) | M | quadratisch | konstant |
| Direktes Einfügen (11.10) | M | quadratisch | konstant |
| Shell-Sort (11.12) | M | > logarithmisch, < quadratisch |
konstant |
| Schnellsort (11.13) | M | logarithmisch | logarithmisch |
| Haldensort (11.14) | M | logarithmisch | konstant |
| Baum (11.19) | M | logarithmisch (entartet: linear) |
linear |
| AVL-Baum (11.22) | M | logarithmisch | linear |
Abb. 11.5: Algorithmen und ihre Komplexität
| © APSIS GmbH |